а) нет решений
б)-2 и 1/3
Объяснение:
а) 9х²+11=0
9х²=-11
9х²=-11
х²=-11/9 - неверно, так как квадрат не может быть отрицательным
ответ: нет решений
б) D=25+24=49
х1,х2=(-5+-7)/6=-2;1/3
f(x)=e^6x-x^2+5
Функція буде зростати на відрізках, де її похідна має додатні значення.
Знаходимо похідну:
f'(x) = 6e^6x-2x ; ця функція неперервна.
Знайдемо точки екстремуму через похідну другого порядку:
f''(x) = 36e^6x-2
36e^6x-2 = 0
18e^6x = 1
6x = ln(1/18)
x = ln(1/18)/6
Дізнаємось знак похідної на точці екстремума:
6e^(6(ln(1/18)/6)) - 2(ln(1/18)/6) = 6e^(ln(1/18)) - (ln(1/18)/3) = 6*1/18 - (ln(1/18)/3) = 1/3 - (ln(1/18)/3) ; ln(1/18) має відємне значення, тому загальний вираз буде додатнім.
Розглянемо похідну на 2 довільних точках по обидві сторони від точки екстремума:
х=0
f'(x) = 6e^(6*0)-2*0 = 6е - значення додатнє
х=-10
f'(x) = 6e^(6*(-10))-2*(-10) = 6e^(-60)+20 = 6/e^60+20 - значення також додатнє
Отже, функція зростає на всій області визначення, крім точки ln(1/18)/6
ответ: а)х∉R b)x1=-2 x2=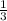
Объяснение:
a) D=-4*9*11
D=-396
b)3x*(x+2)-(x-2)=0
(x+2)*(3x-1)=0
x+2=0
3x-1=0