1
Объяснение:
mn-2m²+3n*(-4m)+4m²=mn-2m²-12mn+4m²=2m²-11mn
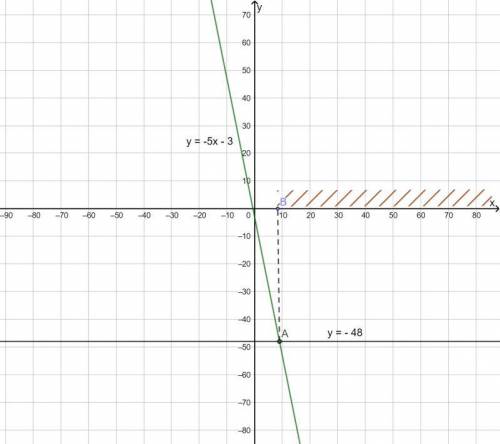
1) При x ≥ 9 значения функции y = -5x - 3 не больше -48.
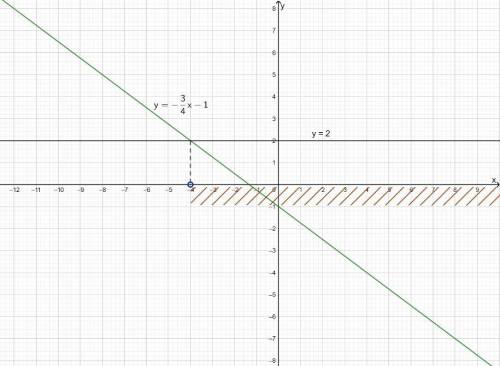
2) При x > -4 значения функции y = -3/4 *x - 1 меньше 2.
Объяснение:
Рисунки прилагаются.
1) y = -5x - 3 линейная функция, график прямая линия, пересекает ось OY в точке (0; --3).
Выберем еще одну точку и построим график функции: x = 10; y = -50-3 = -53.
При каких значениях x значения функции не больше (значит меньше или равно) -48?
Построим в этой же системе координат прямую y = -48.
По графикам видно, что что -5x - 3 ≤ -48 при x ≥ 9
Проверим аналитически:
-5x -3 ≤ -48; -5x ≤ -48 +3; -5x ≤ -45; x ≥ 9.
2) y = -3/4*x - 3 = -0,75x - 1 линейная функция, график прямая линия, пересекает ось OY в точке (0; -1).
Выберем еще одну точку и построим график функции: x = 4;
y = -0,75*4 -1 = -3 - 1 = -4.
При каких значениях x значения функции меньше 2?
Построим в этой же системе координат прямую y = 2.
По графикам видно, что -0,75x - 1 ≤ -2 при x > -4
Проверим аналитически:
-0,75x -1 < 2; -0,75x < 3; x > -4.
ответ:ответ:
Sabcd = 468 см².
Объяснение:
Проведем прямую ВЕ параллельно стороне СD. В параллелограмме ВСDЕ сторона ВЕ = CD = 26см. Сторона DE = ВС = 11 см. Тогда отрезок АЕ равен AD - DE = 28-11= 17см. Полупериметр треугольника АВЕ равен р = (25+26+17)/2 = 34 см. Площадь треугольника АВЕ по Герону равна:
Sabe = √(p(p-AB)(p-BЕ)(p-AЕ) = √(34·9·8·17) = 17·3·4 = 204 см².
Высота этого треугольника = высота трапеции
h = 2·S/AE = 2·204.17 = 24 см.
Площадь трапеции Sabcd = (BC+AD)·h/2 = 39·24/2 = 468 cм².
Или так:
Проведем вторую высоту CF. СА = h. АН = х, FD = (28-11) - x = 17-x.
Тогда в треугольнике АВН по Пифагору: ВН² = 25² - х².
В треугольнике СDF по Пифагору: CF² = 26² - (17-x)². =>
25² - х² = 26² - (17-x)² => 34x = 238. х = 119/17.
Из треугольника АВН по Пифагору:
h² = 25²-(119/17)² = 625 - 14161/289 = 576. =>
h = √576 = 24 см.
Sabcd = (BC+AD)·h/2 = 9·24/2 = 468 cм².
правильный первый вариант