.(1.высота cd прямоугольнова треугольника abc делит гипатинузу ab на части ad=16см и bd=9см. докажите, что треугольник acd приблизительно равин треугольнику cbd и найдите высату cd. 2.точки m и n лежат на сторонах ac и bc треугольник abc ;
ac=16см, bc=12см, cm=12см, cn=9см. докажите, что mn паролельна ab.).
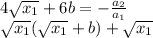
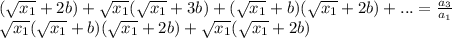
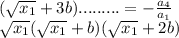
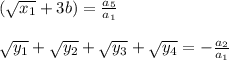
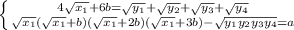
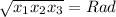, то произведение корней так же число радикальное , откуда с последних двух идет верное равенство
Высота СД разделила треугольник на 2 подобных треугольника АСД и СВД, т.к. у них в каждом есть прямой угол. Это Угол АДС и угол СДВ. Угол САД= Углу ДСВ, как углы с соответственно перпендикулярными сторонами. Треугольники подобны по двум углам. Высота в прямоугольном треугольнике есть среднее пропорциональное между проекциями катетов на гипотенузу. Это следует из пропорции СД: ДВ=АД: СД СД*СД= АД*ДВ =16*9=144 Т.е. СД= 12 см.
2. В треугольниках СМN и АВС есть общий угол С. Поверим пропорциональность сторон АС:СМ= 16:12=4:3 СВ:СN=12:9=4:3. Отношения сторон равны, значит треугольники подобны по двум пропорциональным сторонам и углу между ними. По теореме о пропорциональных отрезках АВ параллельна MN.