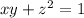относительно 
:
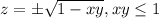
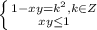
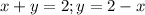
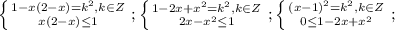
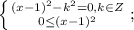
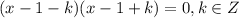
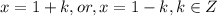
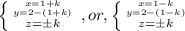
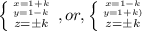
![\frac{a+b+c}{3} \geq \sqrt[3]{abc};a\ \textgreater \ 0;b\ \textgreater \ 0;c\ \textgreater \ 0](/tpl/images/0624/8535/ff736.png)
; 
; 
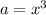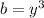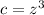
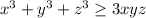
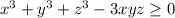
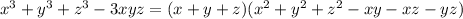
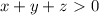по условию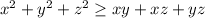
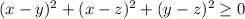
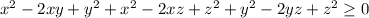
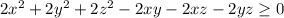
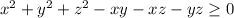
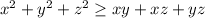
![\frac{a+b+c}{3} \geq \sqrt[3]{abc};a\ \textgreater \ 0;b\ \textgreater \ 0;c\ \textgreater \ 0](/tpl/images/0624/8535/603ee.png)
![a+b+c \geq 3\sqrt[3]{abc}=3* \sqrt[3]{1}=3](/tpl/images/0624/8535/40668.png)
π + 2πk; ±π/3 + 2πk, k ∈ Z.
Объяснение:
1. Область допустимых значений:
1 - cosx ≠ 0;
cosx ≠ 1;
x ≠ 2πk, k ∈ Z.
2. Умножим обе части уравнения на (1 - cosx):
sin2x/(1 - cosx) = 2sinx;
sin2x = 2sinx(1 - cosx).
3. Раскроем скобки и приведем подобные члены:
2sinx * cosx = 2sinx - 2sinx * cosx;
2sinx * cosx - 2sinx + 2sinx * cosx = 0;
4sinx * cosx - 2sinx = 0;
2sinx(2cosx - 1) = 0.
4. Приравняем множители к нулю:
[sinx = 0;
[2cosx - 1 = 0;
[sinx = 0;
[2cosx = 1;
[sinx = 0;
[cosx = 1/2;
[x = 2πk ∉ ОДЗ;
[x = π + 2πk;
[x = ±π/3 + 2πk;
[x = π + 2πk, k ∈ Z;
[x = ±π/3 + 2πk, k ∈ Z.
ответ: π + 2πk; ±π/3 + 2πk, k ∈ Z
х≠5
Д=121-120=1
х1=6
х2=5 не корень
Объяснение: