Окружность с центром в т. O и D = 68. Хорда AB.
Расстояние OM = 30 от т. O до прямой AB.
Найти:AB - ?
Решение:Заметим, что OM ⊥ AB (так как OM - это расстояние от т. О до прямой AB - длина перпендикуляра из точки О к прямой AB).
Пусть отрезок OM лежит на радиусе OC рассматриваемой окружности. Тогда OC, как радиус, перпендикулярный хорде, пересекает эту хорду ровно в ее середине: AM = BM.
Рассмотрим прямоугольные треугольники, равные по первому признаку (или же по двум катетам OM = OM и AM = BM): ΔAOM = ΔBOM.
OA = OB = D / 2 = 68 / 2 = 34, как радиусы.
OM = 30, по условию.
Применим теорему Пифагора, например, к ΔAOM:
AM² + OM² = AO²
AM² = AO² - OM²
AM² = 34² - 30²
AM² = 256
AM = 16
Значит:
AB = AM + BM = AM + AM = 16 + 16 = 32.
Задача решена!
ответ: 32.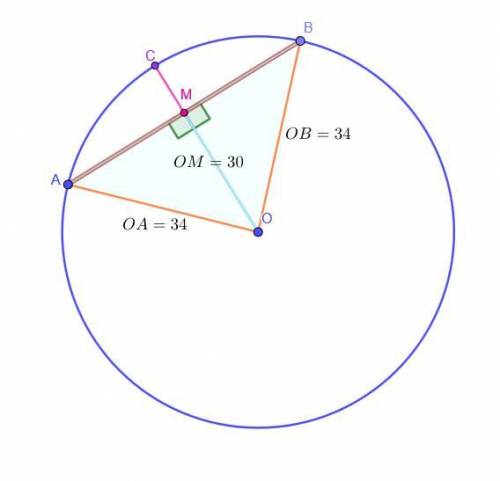
ответ: cos(γ)=0,925, γ≈22°.
Объяснение:
Пусть АВ=2 см, AC=4 см и BC=5 см. Пусть α, β, γ - углы соответственно при вершинах A, B, C треугольника. Для нахождения косинусов углов используем теорему косинусов:
1. BC²=AB²+AC²-2*AB*AC*cos(α), откуда следует уравнение 25=4+16-2*2*4*cos(α), или 25=20-16*cos(α). Отсюда 16*cos(α)=-5 и cos(α)=-5/16. Тогда α=arccos(-5/16)≈108°.
2. AC²=AB²+BC²-2*AB*BC*cos(β), откуда следует уравнение 16=4+25-2*2*5*cos(β), или 16=29-20*cos(β). Отсюда 20*cos(β)=13 и cos(β)=13/20. Тогда β=arccos(13/20)≈49°.
3. AB²=AC²+BC²-2*AC*BC*cos(γ), откуда следует уравнение 4=16+25-2*4*5*cos(γ), или 4=41-40*cos(γ). Отсюда 40*cos(γ)=37 и cos(γ)=37/40. Тогда γ=arccos(37/40)≈22°
Проверка: сумма углов треугольника должна быть равна 180°. В нашем случае α+β+γ≈108°+49°+22°=179°≈180°, так что углы найдены верно.
Таким образом, наименьшим углом является γ. Его косинус равен 37/40=0,925, а его градусная величина - ≈22°.