Здравствуйте!
Вы уже тему квадратных уравнений. Вы знаете, что его стандартный вид ax^2+bx+c=0. Но бывают ещё и квадратные трехчлены. Они отличаются тем, что они не равны нулю и значения х мы найти не можем. Но мы можем упростить такие выражения.
Надо запомнить стандартный вид квадратного трехчлена: ах^2+bx+c.
Как упростить квадратный трехчлен?
Надо найти корни уравнения, где данный трехчлен равен нулю. То есть отдельно приравнять данное выражение к нулю и найти корни. Дальше воспользоваться формулой.
Формула упрощения квадратного трехчлена:
ах^2+bx+c=a(x-x1)(x-x2).
x1 и x2- корни решенного уравнения.
Запомним, что когда уравнение имеет один корень, то оно имеет видоизмененную формулу:
ах^2+bx+c=a(x-x1)^2.
Когда уравнение не имеет корней, его упростить нельзя.
Приступим к практике:
1. Дан квадратный трехчлен x^2-7x+12.
Находим корни уравнения, когда выражение равно нулю:
x^2-7x+12=0
По т. Виета получаем x1= 3; x2= 4.
Подставляем в формулу:
x^2-7x+12=1*(x-3)*(x-4)= (x-3)(x-4).
2. Дан квадратный трехчлен x^2+8x+15.
Находим корни уравнения, когда выражение равно нулю:
x^2+8x+15=0
По т. Виета получаем x1= -3; x2= -5.
Подставляем в формулу:
x^2+8х+15=1*(x-(-5))*(x-(-3))= (x+5)(x+3).
3. Дан квадратный трехчлен 4x^2+3x-22.
Находим корни уравнения, когда выражение равно нулю:
4x^2+3x-22=0
D=9+22*4*4=361
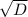 =19
=19
x1=(-3-19)/8=-2,75
x2=(-3+19)/8=2
Подставляем в формулу:
4x^2+3x-22=4*(x-(-2,75))*(x-2)=4 (x+2,75)(x-2).
1) x^2-y^2=9
x-y=1
1. x=1+y
2. (1+y)^2-y^2=9
1+2y+y^2-y^2=9
1+2y=9
2y=8
y=4
3. x=1+y. x=1+4=5
ответ: (5;4)
2 система:
1) x^2+y^2=13
xy=6
1. x=6/y
2. (6/y)^2 + y^2 = 13
36/y^2 + y^2 = 13 (обе части умножаем на y^2, y не равен нулю)
36+y^4 = 13y^2
y^4-13y^2+36=0
y^2=t
t^2-13t+36=0
D=25
t1=9
t2=4
y^2=9, y1=3, y2= - 3
y^2=4, y3=2, y4= - 2
3. x=6/y. x1=2, x2= -2, x3=3. x4= - 3.
ответ: (2;3) (-2;-3) (3;2) (-3;-2)