х ч - выполнял бы работу I каменщик, у ч - II каменщик,
1/х - производительность I каменщика (часть работы, выполняемая за 1 час), 1/у - производительность II каменщика,
12/x - работа выполненная I каменщиком за 12 ч, 12/y - работа выполненная II каменщиком за 12 ч, 12(1/х + 1/у) - работа, выполненая двумя каменщиками за 12 ч,
х/2 ч - выполнял бы половину работы I каменщик, у/2 ч - выполнял бы вторую половину работы II каменщик.
{12(1/x + 1/y)=1,
x/2 +y/2=25;
{12x+12y=xy,
x+y=50,
{y=50-x,
12x+12y-xy=0;
12x+12(50-x)-x(50-x)=0,
x^2-50x+600=0,
D=100,
x1=20,
x2=30;
y1=30,
y2=20.
20 ч и 30 ч
Обозначим Q1 - производительность первой трубы (сколько литров в минуту она пропускает), Q2 - производительность второй трубы
V1-объем 1 резервуара (который заполняет первая труба)
V2 - объем второго резервуара (который заполняет вторая труба)
t1-время за которое первая труба заполнит 1 резервуар
t2- время за которое вторая труба заполнит 2 резервуар
Теперь на основании этого составляем уравнения:
Q1*t1=V1
Q2*t2=V2
Из условий задачи известно, что: Q1=Q2-5
Так же известно, что t2=t1-140 (140 это 2 часа 20 минут в минутах).
Этого достаточно для составления системы уравнений:
Решаем ее: во второе уравнение подставляем Q1+5 вместо Q2 и t1-140 вместо t2
Получаем следующую систему:
Из второго уравнения выражаем t1, получаем: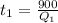
Подставляем в 1 уравнение, получаем:
Первый ответ не подходит, потому что он отрицательный, значит берем второй.
Значит первая труба пропускает Q1=5 л/мин
ответ: первая труба пропускает Q1=5 л/мин