y=4-x^3/x^2
Область определения функции:
х∈(-∞,0)U(0,∞)
Пересечение с осью абсцисс (ОХ):
4-х^3/x^2=0⇔x=∛4
Поведение функции в ограниченных точках области определения:
х=0, limx->0 4-x^3/x^2=∞
Поведение функции на бесконечности:
limx->∞ 4-x^3/x^2=-∞
limx->-∞ 4-x^3/x^2=∞
Наклонная асимптота функции:
у=-х
Исследование функции на четность/нечетность:
f(x)=-x^3-4/x^2
f(-x)=x^3+4/x^2
Функция является не четной, ни нечетной.
Производная функции:
-2*((4-х^3)/х^3)-3
Нули производной:
х=-2
Функция возрастает на:
х∈[-2,0)
Функция убывает на:
х∈(-∞,-2]U(0,∞)
Минимальное значение функции: -∞
Максимальное значение функции: ∞
График во вложениях.
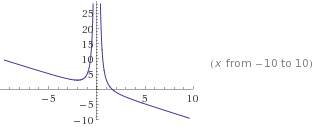
х должен быть больше 0.
Прологарифмируем обе части неравенства по основанию2:
Log (х в степени Log х по осн.2) по основанию 2 (меньше или равно) Log16 по основанию2.
Log х по основанию 2 * Log х по основанию 2 (меньше или равно) 4.
(Log х по основанию 2) в квадрате меньше или равно 4
Пусть Log х по основанию 2 = у
у в квадрате меньше или равно 4
у в квадрате - 4 меньше или равно 0. Решим это неравенство методом интервалов.
(у - 2)(у+2) меньше или равно 0. Отсюда у меньше или равно 2, но больше или равно -2.
Тогда Log х по основанию 2 меньше или равно 2, но больше или равно -2.
или log х по основанию 2 меньше или равно iog 4 по основанию 2, но больше или равно log 1/4 по основанию 2.
Отсюда х меньше или равно 4, но больше или равно 1/4. Удачи!