Объяснение:
15.6
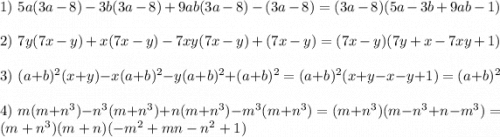
Выносим общую скобку как множитель.
15.9
Тут необходимо сначала разложить на множители, а затем воспользоваться правилом:
Если произведение двух или более множителей равно 0, то хотя бы один из множителей равен 0.
1)
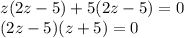
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
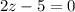 или
или 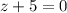
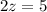 или
или 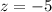
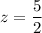 или
или 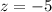
Мы решили! Это и есть ответ!
2)
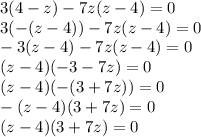
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
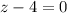 или
или 
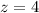 или
или 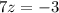
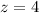 или
или 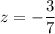
Мы решили! Это и есть ответ!
3)
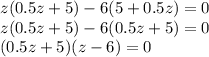
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
 или
или 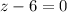
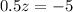 или
или 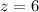
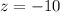 или
или 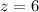
Мы решили! Это и есть ответ!
4)
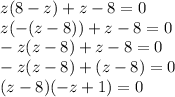
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
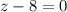 или
или 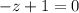
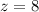 или
или 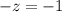
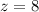 или
или 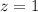
Мы решили! Это и есть ответ!
Обратившись к основному тригонометрическому тождеству, получим:
2sin^2(x) - 5sin(x)cos(x) + 5cos^2(x) = sin^2(x) + cos^2(x);
sin^2(x) - 5sin(x)cos(x) + 4cos^(x) = 0.
Разделим полученное уравнение на cos^2(x):
tg^2(x) - 5tg(x) + 4 = 0.
Произведем замену переменных t = tg(t):
t^2 - 5t + 4 = 0.
Корни квадратного уравнения вида ax^2 + bx + c = 0 определяются
по формуле: x12 = (-b +- √(b^2 - 4 * a * c) / 2 * a.
t12 = (5 +- 3) / 2;
t1 = 1; t2 = 4.
tg(x) = 1;
x1 = π/4 +- π * n.
x2 = arctg(4) +- π * n.
Объяснение: