Второй объем меньше первого на 15,3 %
Объяснение:
Изначально радиус конуса r был 100%. Теперь же его увеличили на 10%, и теперь радиус конуса r₂ равен 110%. Так же это можно записать как:
r₂ = 1,1 × r
Теперь к высоте. С ней все тоже самое, только уменьшили. Значит h = 100%, a h₂ = 70%. То есть h₂ = 0,7 × h
Подставляем новые данные в формулу:
V₂ =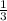 
× π × (1,1 × r)² × 0,7 × h = 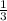× π × 1,21r² × 0,7h
Теперь если поделить V₂ на V₁ (V₁ = 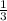× π × r² × h), то получим 0.847, в столько раз второй объем меньше чем первый, или же это можно записать как 100% - 84,7% = 15,3 %
Наибольшее значение функции g(x) на отрезке [0; 2] – 1
Объяснение:
1) Найдём производную данной функции:
g'(x) = 12x-12x^2
2) Найдём нули производной:
12x-12x^2=0
12x(1-x)=0
x1=0 x2=1
3) Определим "поведение" функции на отрезках [0; 1] и [1; 2]:
На отрезке [0; 1] функция возрастает
На отрезке [1; 2] функция убывает
Чтобы найти наибольшее/наименьшее значение первообразной функции, нужно подставить абсциссу точки максимума/минимума в первообразную функцию.
Точкa максимума функции g(x) – 1.
g(1) = 6-4-1 = 1
(
25−a
2
3
+
a
2
−10a+25
1
)∗
a
(5−a)
2
+
a+5
3a
=(
(5−a)
2
∗(a+5)
3∗(5−a)
+
(5−a)
2
∗(a+5)
1∗(a+5)
)∗
a
(5−a)
2
+
a+5
3a
=(
(5−a)
2
∗(a+5)
15−3a+a+5)
)∗
a
(5−a)
2
+
a+5
3a
=(
(5−a)
2
∗(a+5)
20−2a
)∗
a
(5−a)
2
+
a+5
3a
=(
(a+5)a
20−2a
)+
a+5
3a
=(
(a+5)a
20−2a+3a
2
)