проверь задание 5 пример
Объяснение:
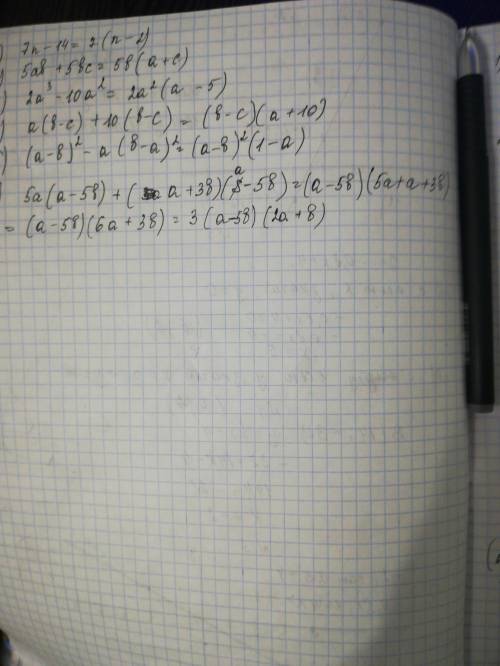
x²+9y⁴+1 ≥ -3xy²-x+3y²
x²+x+1 ≥ -3xy²+3y²-9y⁴
x²+x+1 ≥ -3y²(x-1+y²)
y²≥0 за будь-якого значення у
⇒ -3y²≤0
Знайдемо вершину параболи f(x)=x²+x+1
xo= -b/2a = -1/2= -0,5
f(xo)= 0,25-0,5+1=0,75
Вітки параболи напрямлені вгору, адже а>0, отже в такому випадку значення виразу x²+x+1 завжди додатнє (бо функція завжди додатня)
Тоді x²+x+1>0 за будь-якого значення х
1)Якщо у=0, x-будь-яке число, то -3y²=0 ⇒ -3y²(x-1+y²)=0
Як вказано раніше, x²+x+1>0
Будь-яке додатнє число більше нуля, отже й
x²+x+1 > -3y²(x-1+y²) ⇒ x²+9y⁴+1 ≥ -3xy²-x+3y²
2) Якщо х=0, y≠0,
З іншого боку, нерівність можна перетворити на таку:
x²+x+3xy² ≥ 3y²-9y⁴-1
х(x+1+3y²) ≥ 3y²-9y⁴-1
Якщо один із множників--нуль, то і весь вираз дорівнює нулю:
Необхідно довести, що
3y²-9y⁴-1 ≤ 0
-(3y²)²+3y²-1 ≤ 0
y⁴≥0
Заміна: 3y²=n, n>0
-n²+n-1≤ 0
f(n)= -n²+n-1
no= -1/-2 = 1/2= 0,5
f(no)= -0,25+0,5-1 = -0,75
Вітки параболи напрямлені вниз, бо а<0
Отже, -n²+n-1≤ 0 ⇒ 3y²-9y⁴-1≤0
х(x+1+3y²) ≥ 3y²-9y⁴-1 ⇒ x²+9y⁴+1 ≥ -3xy²-x+3y²
3) Якщо х>0, y≠0
x²+x+3xy² ≥ 3y²-9y⁴-1
x²≥0
Як зазначено раніше, 3y²-9y⁴-1<0
Відомо, що x²>0, 3y²>0
Оскільки х--додатнє число, то 3xy²>0
При додаванні додатніх чисел результат теж додатній: x²+x+3xy²>0
Додатнє число завжди більше за від'ємне, тож
x²+x+3xy² > 3y²-9y⁴-1 ⇒ x²+9y⁴+1 ≥ -3xy²-x+3y²
4) Якщо х<0, y≠0
x²+x+3xy² ≥ -9y⁴+3y²-1
Заміна: 3y²=n, n>0
f(x)=x²+x(1+n)
b=1+n
коефіцієнт b не впливає на зміщення по ординаті, а коефіцієнта с в наданій квадратичній функції немає. Також вітки параболи напрямлені вгору, бо а>0.
Таким чином, x²+x(1+n)>0, а -n²+n-1<0, тому x²+x(1+n)>-n²+n-1<0 ⇒ x²+x+3xy² ≥ -9y⁴+3y²-1 ⇒ x²+9y⁴+1 ≥ -3xy²-x+3y²
Нерівність доведено
1) Если принять за Х количество дней за которые планировалось изготовить все детали (изготавливая по 20 дет. в день), то количество деталей можно выразить как 20Х. Каждый день рабочий фактически делал не 20, а 20+8=28 деталей и изготовил (20Х+8) деталей за (Х-2) дня. Поэтому можно записать уравнением:
28(Х-2)=20Х+8
28Х-20Х=8+56
Х=64/8=8
Задание рабочий должен был выполнить за 8 дней (при этом изготовить 20*8=160 деталей, изготавливая по 28 дет. в день за 8-2=6 дней он сделал 28*6=168 деталей, т.е. на 8 больше).
2) Аналогичная задача: по 10 зад. в день нужно делать Х дней, всего задач будет 10Х. Если делать по 10+4=14 задач за Х-3 дня то нужно еще сделать 2 задачи, чтобы стало 10Х, уравнение принимает вид:
14(Х-3)+2=10Х
14Х-10Х=42-2
Х=40/4=10
Если решать 10 дней по 10 задач, то всего нужно решить 10*10=100 задач. (Если решать по 14 задач 10-3=7 дней, то останется решить 2 задачи: 14*7=98 зад., 100-98=2 зад.).
3) Если представить условно двузначное число в виде цифр (ав), то его можно математически выразить в форме а*10+в. Обратное выражение (ва) - это в*10+а. Известно, что соблюдаются два условия:
(а*10+в) - 54= в*10+а и а=3в, решаем данную систему уравнений, подставив второе выражение в первое.
3в*10+в-54=10в+3в
в=54/18=3
а=3в=3*3=9,
ответ: двузначное число - это 93
1. 7n-14=7(n-2)
2. 5ab+5bc=5b(a+c)
3. 2a^3-10a^2=2a^2(a-5)
4. a(b-c)+10(b-c)=(b-c)(a+10)
дальше не знаю,извини