ответ:a) – 6a3(a2 – 8a – 7)=-6a5+48a4+42a3
б) (х – 5)(3y + 2*2)=3xy+4x-15y-20
в) (7 – 4х)2=16x2-56x+49
Объяснение:
a) -6a3(a2-8a-7)=-6a3*a2-6a3(-8a)-6a3(-7)=-6a5+48a4+42a3
б) (x-5)(3y+2*2)=(x-5)(3y+4)=3xy+4x-15y-20
в) (7-4x)2=49-56x+16x2=16x2-56x+49
Чтобы найти значение выражения а * ( а + b ) ^ 2 + 2 * a * ( a ^ 2 + b ^ 2 ) - a * ( a - b ) ^ 2 при а = 2 , 5 и b = 0 , 5, надо выражение сначала упростить, потом известные значения подставить в само выражение. То есть получаем:
а * ( а + b ) ^ 2 + 2 * a * ( a ^ 2 + b ^ 2 ) - a * ( a - b ) ^ 2 = a * ( a ^ 2 + 2 * a * b + b ^ 2 ) + 2 * a ^ 3 + 2 * a * b ^ 2 - a * ( a ^ 2 - 2 * a * b + b ^ 2 ) = a ^ 3 + 2 * a ^ 2 * b + a * b ^ 2 + 2 * a ^ 3 + 2 * a * b ^ 2 - a ^ 3 + 2 * a ^ 2 * b - b ^ 2 * a = 4 * a ^ 2 * b + 2 * a ^ 3 + 2 * a * b ^ 2 = 4 * 2 . 5 ^ 2 * 0 . 5 + 2 * 2 . 5 ^ 3 + 2 * 2 . 5 * 0 . 5 ^ 2 = 12 . 5 + 31.25 + 1.25 = 45.
2
Объяснение:
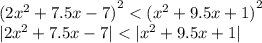
Рассмотрим 4 случая, когда выводим выражения из модулей:
1) 1ое и 2ое выражения положительные
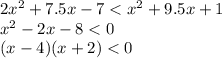
т.е. ответ -1+0+1+2+3=5
2) 1ое положительное и 2ое отрицательное

т.е. ответ -5-4-3-2-1+0=-15
3) 1ое отрицательное и 2ое положительное
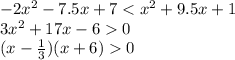
т.е. область будет лежать в окрестностях (-бесконечность;-6) и (1/3;+бесконечность) в ответе сумма всех целых чисел: 1+2+3+4+5=15 т.к. остальные числа взаимно сокращаются
4) 1ое и 2ое отрицательные
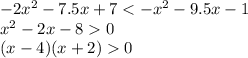
т.е. область в окрестностях (-бесконечность;-2) и (4;+бесконечность). В ответе сумма всех целых чисел дает: -3 аналогично
Тогда, если суммировать все ответы в 4 случаях: 5-15+15-3=2
Нужно перемножить, раскрыв скобки:
А. - 6a3(a2 - 8a - 7) = - 6а5 + 48а4 +42а3.
Б. (х - 5)(3y + 2x2) = 3ху + 2х3 - 15у - 10х2.
В. (7 - 4х)2 = 49 - 56х + 16х2.