ответ на задание:
В системе приведены уравнения двух прямых, раз система имеет единственное решение, то прямые имеют только 1 общею точку, а значит они пересекаются.
ответ: 2) пересекаются.
Просто факт про прямые:
Прямые a₁x+b₁y=c₁; a₂x+b₂y=c₂
Параллельны, если a₁/a₂ = b₁/b₂ ≠ c₁/c₂
Пересекаются, если a₁/a₂ ≠ b₁/b₂
Совпадают, если a₁/a₂ = b₁/b₂ = c₁/c₂
В нашем случаи 2/2 ≠ -3/3 ⇒ прямые пересекаются.
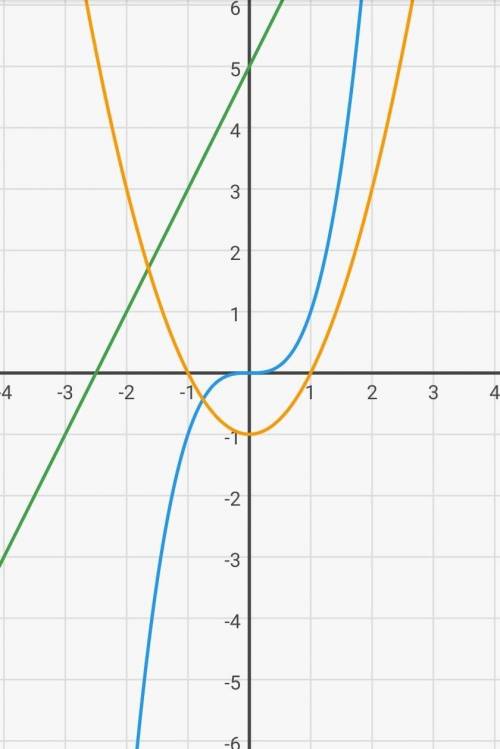
1. голубая (кубическая парабола; для того чтобы построить её можно использовать таблицу значений.
x | -2 | -1 | 0 | 1 | 2 |
——————————>х
y | -8 | -1 | 0 | 1 | 8 |
Отмечаем эти точки на координатной прямой, и соединяем плавной линией, без углов как на рисунке.
2. Зелёная (Прямая; чтобы построить такой график используем таблицу значений
x | -5 | -4 | -3 | -2 | -1 | 0 | 1
——————————————>х
y | -5 | -3 | -1 | 1 | 3 | 5 | 7
также нужно вместо икса подставитьзначения R.)
3. Оранжевая. (парабола, строим график y=x² и опускаем на 1 вниз.)
или составим таблицу функции y=x²-1
x | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5
—————————————————————>х
y | 24| 15 | 8 | 3 | 0 | -1 | 0 | 3 | 8 | 15| 24
В решении.
Объяснение:
На одном садовом участке в 3 раза больше кустов мялины, чем на другом. После того как с первого участка пересадили на второй 31 куста, на обоих участках кустов мялины стало поровну. Сколько кустов мялины было на каждом участке?
х - было кустов на 2 участке.
3х - было кустов на 1 участке.
3х-31 - стало кустов на 1 участке.
х+31 - стало кустов на 2 участке.
По условию задачи кустов стало поровну, уравнение:
3х-31 = х+31
3х-х=31+31
2х=62
х=31 - было кустов на 2 участке.
31*3=93 - было кустов на 1 участке.
Проверка:
93-31 = 31+31
62 = 62, верно.
По моему параллельным