не уверена, но вот :
-х²=2х-3
-х²-2х+3=0
х²+2х-3=0
х²+3х-3=0
х(х+3)-х-3=0
х(х+3)-(х+3)=0
(х+3)(х-1)=0
х+3=0
х-1=0
х=-3
х-1=0
х=-3
х=1
х1=-3; х2=1
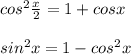
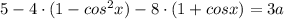
Получаем квадратное уравнение относительно
cosx=t
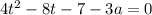
Это уравнение имеет хотя бы один корень, если D ≥0
D=64+16(7+3a)=16(11+3a)
D≥0⇒ 11+3a≥0⇒ a≥ -11/3
t₁=1- (√(11+3а))/2 или t₂=1+ (√(11+3а))/2
Обратная замена приводит к уравнениям вида cos=t₁ или cosx=t₂
Чтобы эти уравнения имели хотя бы один корень, необходимо, что бы
-1 ≤ t₁ ≤1 или -1 ≤ t₂ ≤1
Решаем неравенства:
-1 ≤1+ (√(11+3а))/2 ≤1
-2≤√(11+3а))/2≤0
-4≤√(11+3а)≤0
Решением неравенства является
11+3a=0
a=-11/3
t₁=t₂=1/2
cosx=1/2
x=±(π/3)+2πn, n∈Z
Неравенство
-1 ≤1- (√(11+3а))/2 ≤1
также приводит к ответу a=-11/3
О т в е т. При а=-11/3
x=±(π/3)+2πn, n∈Z
а) Подставляем в выражение функции значение Х, получаем У.
у= -4*0,5 + 10
у= -2 +10
у= 8
б) Подставляем в выражение функции значение У, получаем Х.
2= -4х + 10
4х=10 - 2
4х= 8
х = 2
в) Подставить в выражение функции значение Х и посмотреть, чему будет равен У.
у = -4х + 10
у = -4*-5 + 10
у = 20 + 10
у = 30 (как в условии) Да, проходит.
2) Чтобы построить график функции, нужно найти точки, по которым его строить (линейная функция - это прямая).
Придаём значения Х, получаем значения У.
0 2
1 7
-1 -3
Через эти три точки (0;2) (1;7) (-1; -3) проводим прямую.
а) Как в первом задании под пунктом в)
у = 5 * -12 +2
у = -60 +2
у = -58 (в условии у=74) Нет, не проходит.
б) Можно найти на графике, а можно вычислить:
У = 7 У = 0
7=5х+2 0=5х+2
-5х=2-7 -5х=2
-5х=-5 5х=-2
5х=5 х=-0,4
х=1
3) Построить график. Придаём значения Х, получаем значения У
0 0
5 -4
По найденным двум точкам (0;0) (5; -4) строим прямую.
4) Чтобы найти координаты точки пересечения графиков двух линейных функций, нужно приравнять правые части уравнений, решить, как простое уравнение, найти значения Х и У, это и будут координаты точки пересечения этих функций.
Объяснение:
-x²=2x-3=x1=-3,x2=1
Объяснение:
-x²=2x-3=
-x²-2x+3=0
x²+2x-3=0
x²+3x-x-3=0
x(x+3)-(x+3)=0
(x+3)(x-1)
x+3=0
x-1=0
x=-3
x=1
ответ: x1=-3
x2=1