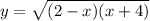
Подкоренное выражение корня чётной степени должно быть неотрицательным, то есть ≥ 0 . Значит :
(2 - x)(x + 4) ≥ 0
(x - 2)(x + 4) ≤ 0
+ - +
__________[- 4]____________[2]___________
/////////////////////////////
Область определения : все x ∈ [ - 4 ; 2]

|y
|x
| .
| .
| .
| .
| .
| .
0
(ось у сплошной. соединишь точки - получишь график - ветвь параболы, лежащая на боку)
а) наиб. и наим. значение находим через производную
(-√x)'=-1/(2√x)
приравниваем к нулю -1/(2√x)=0. нет корне. находим значение функции на концах отрезка.
y(1)=-1
y(6)=-√6
-1 наиб. знач.
б) так как пересекаются, значит х1=х1, у1=у2
y*y+3+4y=0
D=16-12=4
y1=(-4+2)/2=-1
y2=-3
оба подходят
находим х1 и х2
х1=1
х2=9
ответ:а)-1, б)(1;-1), (9:-3).
√(2-х)(х+4) = √(2х-х²+8-4х) =
√(-х²-2х+8).
-х²-2х+8 ≥ 0;
d = 36.
х1 = -4;
х2 = 2.
---(-)--(-4)--(+)(2)-(-)---→x
ответ: [-4;2].