Представьте произведение(4,5 105)(2,5 10-8) в стандартном виде.
очень

👇

Увидеть ответ

Ответ:

Girlverysilly098887

16.04.2021

(4,5 *10⁵)(2,5 *10⁻⁸)=4.5*2.5*10⁻³=11.25*10⁻³=1.125*10⁻²

4,6(75 оценок)

Открыть все ответы

Ответ:

срочно118

16.04.2021

Пусть сторона квадрата х см, тогда длина прямоугольника (3х) см, а ширина прямоугольника - (х - 5) см.

Т.к. площадь квадрата находят по формуле S = а², где а - сторона квадрата, о площадь данного квадрата равна (х²) см².

А т.к площадь прямоугольника находят по формуле S = a · b, где a и b - длина и ширина прямоугольника, то площадь данного прямоугольника будет равна S = 3х · (х - 5) = 3х² - 15х (см²).

Т.к. площадь квадрата на 50 см² меньше площади прямоугольника, то составим и решим уравнение:

3x² - 15х = x² + 50,

3x² - x² - 15x - 50 = 0,

2x² - 15x - 50 = 0,

D = (-15)² - 4 · 2 · (-50) = 225 + 400 = 625 ; √625 = 25,

x₁ = (15 + 25)/(2 · 2) = 40/4 = 10,

x₂ = (15 - 25)/(2 · 2) = -10·/4 = -2,5 - не подходит по условию задачи.

Значит, сторона квадрата равна 10 см.

ответ: 10 см.

4,5(71 оценок)

Ответ:

Danfdffefd

16.04.2021

Исходное неравенство распадается на совокупность систем:

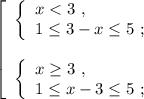
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 3 \ , \\ 1 \leq 3-x \leq 5 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 3 \ , \\ 1 \leq x-3 \leq 5 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} \left\{\begin{array}{l} x < 3 \ , \\ -5 \leq x-3 \leq -1 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 3 \ , \\ 1+3 \leq x \leq 5+3 \ ; \end{array}\right \end{array}\right$

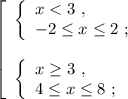
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 3 \ , \\ -2 \leq x \leq 2 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 3 \ , \\ 4 \leq x \leq 8 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} x \in [ -2 ; 2 ] \ , \\ x \in [ 4 ; 8 ] \ ; \end{array}\right$

$x \in [ -2 ; 2 ] \cup [ 4 ; 8 ] \ ;$

а) неравенство эквивалентно:

$-2 \leq x \leq 2 \ ;$

$x \in [ -2 ; 2 ] \ ;$

Отрезок данного решения полностью совпадает с одним из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет 1/2 .

о т в е т :    $\frac{1}{2} = 0.5 = 50 \% \ ;$

б) неравенство эквивалентно:

$-2 \leq x-6 \leq 2 \ ;$

$6-2 \leq x \leq 2+6 \ ;$

$x \in [ 4 ; 8 ] \ ;$

Отрезок данного решения полностью совпадает с одним из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет 1/2 .

о т в е т :    $\frac{1}{2} = 0.5 = 50 \% \ ;$

в) неравенство эквивалентно:

$-1 \leq x \leq 1 \ ;$

$x \in [ -1 ; 1 ] \ ;$

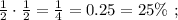
Отрезок данного решения составляет половину от одного из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет    $\frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4} = 0.25 = 25 \% \ ;$

о т в е т :    $\frac{1}{4} = 0.25 = 25 \% \ ;$

г) неравенство распадается на совокупность систем:

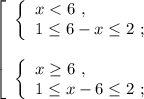
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 6 \ , \\ 1 \leq 6-x \leq 2 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 6 \ , \\ 1 \leq x-6 \leq 2 \ ; \end{array}\right \end{array}\right$

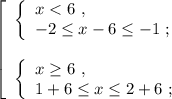
$\left[\begin{array}{l} \left\{\begin{array}{l} x < 6 \ , \\ -2 \leq x-6 \leq -1 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 6 \ , \\ 1+6 \leq x \leq 2+6 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} \left\{\begin{array}{l} x < 6 \ , \\ 4 \leq x \leq 5 \ ; \end{array}\right \\\\ \left\{\begin{array}{l} x \geq 6 \ , \\ 7 \leq x \leq 8 \ ; \end{array}\right \end{array}\right$

$\left[\begin{array}{l} x \in [ 4 ; 5 ] \ , \\ x \in [ 7 ; 8 ] \ ; \end{array}\right$

$x \in [ 4 ; 5 ] \cup [ 7 ; 8 ] \ ;$

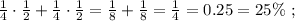
Каждый из двух отрезков данного решения составляет четверть от одного из равных (по дине) отрезков, которые генерируют переменную. А значит, вероятность составляет    $\frac{1}{4} \cdot \frac{1}{2} + \frac{1}{4} \cdot \frac{1}{2} = \frac{1}{8} + \frac{1}{8} = \frac{1}{4} = 0.25 = 25 \% \ ;$

о т в е т :    $\frac{1}{4} = 0.25 = 25 \% \ ;$

4,4(14 оценок)

Это интересно:

Хобби-и-рукоделие

03.01.2020

Как легко стать ниндзя: советы от профессионалов...

Искусство-и-развлечения

27.05.2020

Колыбель для кошки: правила игры и советы для начинающих...

Семейная-жизнь

26.12.2020

Правильное питание для мам, кормящих грудью: Как справиться с диетой...

Дом-и-сад