Группа точек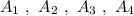 
имеют одинаковую абсциссу х=4 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 
.
.
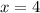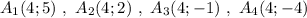Группа точек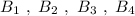 
имеют одинаковую абсциссу х=2 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 
.
.
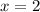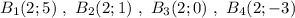Группа точек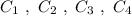 
имеют одинаковую абсциссу х= -2 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 
.
.
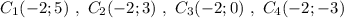Группа точек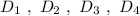 
имеют одинаковую абсциссу х= -4 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 
.
.
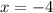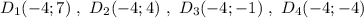Точки, имеющие одинаковую абсциссу, на координатной плоскости лежат на одной прямой, параллельной оси ОУ.
Уравнение такой прямой имеет вид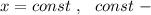 
это число (константа- постоянная величина ) .
ответ: 10.
Объяснение:
Находим производную y'=3*x²-12*x+12 и приравниваем её к нулю. После сокращения на 3 получаем квадратное уравнение x²-4*x+4=(x-2)²=0, откуда x=2 - единственная критическая точка. Но так как производная y' везде, кроме точки x=2, положительна, то есть не меняет знак при переходе через точку x=2, то эта точка не является точкой экстремума. И так как y'≥0, то функция y монотонно возрастает (в широком смысле) на всей области определения, которой является вся числовая ось. Поэтому наибольшее значение функция принимает в "правом" конце интервала [0;3], т.е. при x=3. Оно равно y(3)=3³-6*3²+12*3+1=10