1) х₁=0, х₂=5, х₃=-5
2) х=1/12
3) х₁=3, х₂=4, х₃=-4.
Объяснение:
1) 4x³-100x = 0
Выносим общий множитель - 4х - за скобки.
4х(х²-25)=0
Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю.
4х=0
х=0
х²-25=0
х²=25
х=±√25
х=±5
ответ: х₁=0, х₂=5, х₃=-5.
2) 144x^3-24x^2+x=0
Выносим общий множитель - х - за скобки.
х(144х²-24х+1)=0
х=0
144х²-24х+1=0
Квадратное уравнение решаем через дискриминант.
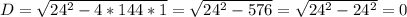
Уравнение будет иметь один корень, т.к. дискриминант равен нулю.
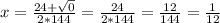
ответ: х=1/12.
3) x³-3x²-16x+48=0
Сгруппируем.
(х³-3х²)+(-16х+48)=0
Из первой скобки вынесем общий множитель х², а из второй (-16).
х²(х-3)-16(х-3)=0
Вынесем за скобки общий множитель (х-3).
(х-3)(х²-16)=0
х-3=0
х=3
х²-16=0
х²=16
х=±√16
х=±4
ответ: х₁=3, х₂=4, х₃=-4.
1) 5x² + 30x + 45 = 5*( x² + 6x + 9 ) = 5*( x + 3 )*( x + 3 )
2) 10x² - 90 = 10*( x² - 9 ) = 5*2*( x - 3 )*( x + 3 )
3) cокращаем числитель и знаменатель дроби на 5*( x + 3 )
4) получаем ( x + 3 ) / ( 2*( x - 3 )) = ( x + 3 ) / ( 2x - 6 )
ОТВЕТ ( x + 3 ) / ( 2x - 6 )
N 2
( x² + 25 )/( x² - 25 ) + ( 5 / ( 5 - x ) = ( x² + 25 - 5( x + 5 )) / ( x² - 25 ) =
= ( x² + 25 - 5x - 25 ) / ( x² - 25 ) = ( x² - 5x ) / ( x² - 25 ) = ( x*( x - 5 )) /
/ ( ( x - 5 )*( x + 5 )) = x / ( x + 5 )
ОТВЕТ x / ( x + 5 )