1.
График в нашей жизни
.
2.
Цель
Выяснить , действительно ли нас
повсюду окружают графики.
3.
Для чего нужны графики ?
Графики, как и любая графическая информация,
позволяют визуализировать информацию.
Превратить сухие цифры из отчетов, таблиц в
наглядную, понятную информацию.
4.
Где встречается графики ?
На уроках математики .
● На уроках географии (график
колебания температуры ) .
● Текущие курсы валют .
● На больницах.
● График роста народонаселения .
● В разных профессиях
( бухгалтера,экономиста,инженера) .
5.
Рене Декарт
1596-1650 г.
Французский
математик и филосов
XVII века,
составитель
знаменитого трактата
<<Геометрия>>
(1637) где в первые
был изложен график .
6.
Графики в реальной жизни
Яблоко растёт, затем его срывают и
сушат. ( х – время; у – масса яблока)
7.
Медицина и графики
Кардиограмма
Кардиограф Врачи
выявляют болезни
сердца, изучая
графики,
полученные с
кардиографа, их
называют
кардиограммами.
8.
Термограф
9.
График температуры
10.
Сейсмограф
Сейсмограф Используя
показания сейсмографов
(приборов непрерывно
фиксирующих колебания
почвы и строящих
специальные графики сейсмограммы) геологи
могут предсказать
приближение землетрясения
или цунами.
11.
Графики в экономике
Широко
применяются
графики в экономике,
в частности кривая
спроса и
предложения, линия
производственных
возможностей.
Графики в экономике.
12.
Вывод
Наши дни невозможно
представить без
графиков , ведь это
неотъемлемая часть
некоторых
профессий .
Равенство квадратной функции обладает единый тип:
около = ах^2 + вх + со, в каком месте но, во также со коэффициенты.
Так Как выискиваемая роль обязана протекать посредством места Но, Во также Со, в таком случае их местоположение обязаны концентрировать равенство функции во правильное равноправие.
Подставим во равенство квадратной функции местоположение данных пунктов также найти решение приобретенную концепцию уравнений сравнительно коэффициентов:
3 = но * (- 3)^2 + во * (- 3) + со;
9а - 3в + со = 3; (1)
3 = но * 1^2 + во * 1 + со;
но + во + со = 3; (2)
8 = но * (- 4)^2 + во * (- 4) + со;
16а - 4в + со = 8; (3)
Сформулируем с (2) но также подставим во (1) также (3):
но = 3 - во - со;
9 * (3 - во - со) - 3в + со = 3;
27 - 9в - 9с - 3в + со = 3;
12в + 8с = 24;
3в + 2с = 6; (4)
16 * (3 - во - со) - 4в + со = 8;
48 - 16в - 16с - 4в + со = 8;
20в + 15с = Сорок;
4в + 3с = 8; (5)
Отнимем с (5) (4)
4в + 3с - 3в - 2с = 8 - 6;
во + со = 2; (6)
Обнаружим но:
но = 3 - 2 = 1.
Сформулируем с (6) во также подставим во (5):
во = 2 - со;
4(2 - со) + 3с = 8;
8 - 2с + 3с = 8;
со = 0;
во = 2 - 0 = 2.
Таким Образом, квадратная роль обладает тип:
около = х^2 + 2х.
Объяснение:
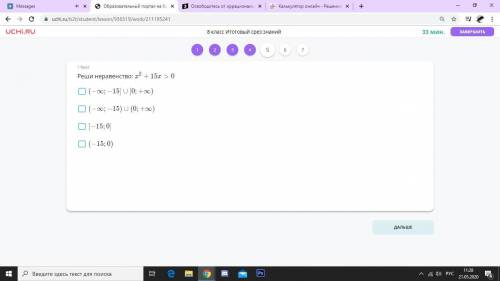
ответ:(-беск: -15(вкл))
Объяснение:
x2+15x>0
x выносим за скобку
x(x+15)>0
=>
x>0
x+15>0
метод интервалов.
x+15=0
x=-15
+ -15 -
(-беск:-15 (вкл))