Наш многочлен имеет вид
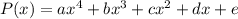
Пусть меньший его корень равен 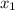 . Так как корни образуют арифметичекую прогрессию, можем записать:
. Так как корни образуют арифметичекую прогрессию, можем записать:
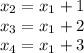
Многочлен раскладывается на линейный множители следующим образом:
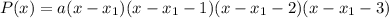
Напрашивается замена 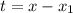 . Тогда
. Тогда
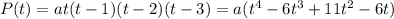
Нам нужно найти минимумы этой функции, поэтому дифференцируем:
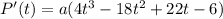
Теперь требуется найти корни этого многочлена. Используя теорему о рациональных корнях многочлена можно найти корень 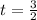
Согласно теореме Безу, 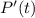 должен делиться на
должен делиться на 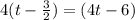 . Разложим на множители, чтобы найти остальные корни:
. Разложим на множители, чтобы найти остальные корни:
![P'(t)=a(4t^3-6t^2-12t^2+18t+4t-6)=a[t^2(4t-6)-3t(4t-6)+(4t-6)]=a(4t-6)(t^2-3t+1)](/tpl/images/0952/7803/88744.png)
Решив квадратное уравнение 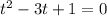 , найдем корни
, найдем корни
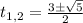
Расположив корни
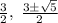
на числовой прямой и использовав метод интервалов, узнаем, что производная меняет знак с минуса на плюс в точках 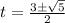 , это и есть точки минимума. Переходя обратно к многочлену от x, получаем точки
, это и есть точки минимума. Переходя обратно к многочлену от x, получаем точки
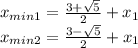
Квадрат расстояния между ними:
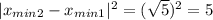
Давайте разберемся.
Пусть некоторое A - утверждение. Будем называть утверждением некоторое предположение, которое характеризуется либо как истинное и тогда утверждение равняется единице, либо как ложное и тогда утверждение равняется нулю.
В данном случае за утверждение принимается:
A - предположение, говорящее, что Первая буква гласная.
B - предположение, говорящее, что Последняя буква согласная.
Немного об операциях в т.н. алгебре логики (термин сложный и его нужно разъяснять отдельно, делается это в курсе т.н. "высшей алгебры").
Это сложение (известное также как объединение в теории множеств) и умножение (пересечение). Здесь их называют логическое "ИЛИ" (дизъюнкция) и логическое "И" (конъюнкция). Раз уж речь идет об алгебре, то, конечно, имеем также логическое "НЕ". По аналогии с теорией множеств, это дополнение к какому-то операнду (а суть унарная операция, интересная вещь).
Давайте запишем как нужно само выражение.
-A∧-B (вместо минусов нужно черточку над буквой).
Таблица истинности выглядит так:
В наименованиях столбцов пишите A и B и ваше выражение третьим.
Затем подставляете различные наборы значение A и B, A и B принимают только значения 0 и 1. Получаете соответственно 0 или 1.
"НЕ" - значит, утверждение обращается - было 1, стало 0, и наоборот.
"И" - дает 1 если оба операнда 1, иначе дает 0.
"ИЛИ" - дает 0 если оба операнда 0, иначе дает 1.
Вот и все. Заполняете и получаете нужное.