1. Б
2. Г
3. В
4. 1) у(2) = 8 * 2 - 3 =13
2) -19 = 8x - 3
-19 + 3 = 8x
8x = -16
x = -2
3) -13 = 8 * (-2) - 3
-13 = -16 - 3
-13 ≠ -19
Графік не проходить через точку А
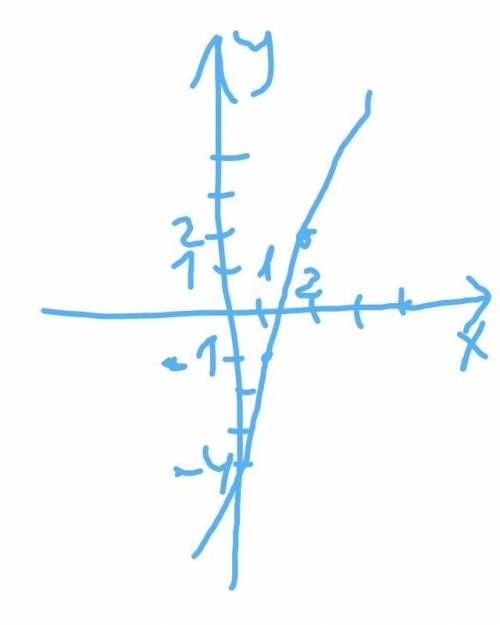
5. х>0 при х=(1 1/3; + ∞)
6. 6х² - 3х ≠ 0
3х(2х - 1) ≠ 0
х ≠ 0; 2х ≠ 1
х ≠ 0; х ≠1/2
D(y) = ( -∞; 0)∪(0; 1/2)∪(1/2; +∞)
7. y = 47x - 9 та y = -13x + 231
47x - 9 = -13x + 231
47x + 13x = 231 + 9
60x = 240
x = 4
y(4) = -13 * 4 +231 = 179
(4; 179)
8. Нехай невідома функція у = kx + b.
Якщо вона паралельна графіку у = -5х + 8 , то k = -5.
Тоді невідома функція у = -5х + b.
Оскільки графіку даної функції належить точка В(-2; 8), то
8 = -5 * (-2) + b
8 = 10 + b
b = 8 - 10
b = -2
Відповідь: у = -5х - 2
В решении.
Объяснение:
Представьте в виде многочлена выражение:
(0,8a + 0,9b)(0,8a - 0,9b) = 0,64a² - 0,81b².
Представьте в виде многочлена выражение:
(8x⁴+9y)(8x⁴−9y) = 64х⁸ - 81у².
Разложите на множители:
0,01m⁶−2,56n⁶ = (0,1m³ - 1,6n³)(0,1m³ + 1,6n³).
Разложите на два множителя:
36x²−1,21y² = (6х - 1,1у)(6х + 1,1у).
Представьте в виде многочлена выражение:
(0,4a+3b)(0,4a−3b) = 0,16a² - 9b².
Выполните умножение многочленов:
(2a²+0,1)(2a²−0,1) = 4a⁴ - 0,01.
Разложите на два множителя:
49m²−289n² = (7m - 17n)(7m + 17n).
Разложите на множители:
a⁴−0,16b⁴ = (a² - 0,4b²)(a² + 0,4b²).
Выполните умножение многочленов:
(0,3x+6)(0,3x−6) = 0,09x² - 36.
Разложите на множители:
0,49m⁶−225n⁶ = (0,7m³ - 15n³)(0,7m³ + 15n³).
Разложите на два множителя:
0,09x²−1,96y² = (0,3x - 1,4y)(0,3x + 1,4y).
Представьте в виде многочлена выражение:
(7x⁴+0,8y³)(7x⁴−0,8y³) = 49x⁸ - 0,64y⁶.
Выполните возведение в квадрат:
(1,6+0,5a)² = 2,56 + 1,6a + 0,25a².