1) Выделяем полные квадраты:
для y: (y²+2*7y + 72) -1*72 = (y+7)²-49
Преобразуем исходное уравнение:
(y+7)² = 6x - 0
Получили уравнение параболы:
(y - y0)² = 2p(x - x0)
(y+7)² = 2*3(x - 0)
Ветви параболы направлены вправо, вершина расположена в точке (x0, y0), т.е. в точке (0;-7)
Параметр p = -3.
Координаты фокуса: F(-p/2; yo) = (-1,5; -7).
Уравнение директрисы: x = x0 - p/2
x = 0 - 3/2 = -3/2.
2) Выделяем полные квадраты:
для x: (x²-2*1x + 1) -1 = (x-1)²-1
для y: -4(y²+2*3y + 3²2) +4*3² = -4(y+3)²+36
В итоге получаем:
(x-1)²-4(y+3)² = -68
Разделим все выражение на -68
(-1/68)(x - 1)² + (1/17)(y + 3)² = 1.
Параметры кривой.
Данное уравнение определяет гиперболу с центром в точке:
C(1; -3)
и полуосями: a = 2√17, b =√17.
Найдем координаты ее фокусов: F1(-c;0) и F2(c;0), где c - половина расстояния между фокусами
Определим параметр c: c² = a² + b² = 68 + 17 = 85
c = √85.
Тогда эксцентриситет будет равен: e = c/a = √85/2√17.
Асимптотами гиперболы будут прямые: y + 3 = (1/2)(x - 1) и
y + 3 = (-1/2)(x - 1).
Директрисами гиперболы будут прямые: +-е/а = +-(√68/√85).
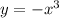
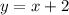
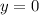
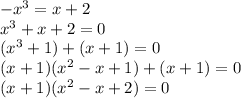
Объяснение:
1)5х+3х=14+0
8х=14
Х=14 : 8
Х=1,75
2)2у+у=2+4
3у=6
У=6 : 3
У=2
3)первое уравнение домножаем на 2, получается :
8х-10у=12
2х+10у=21
(У сокращаются), остаётся:
8х+2х=12+21
10х=33
Х=3,3
Ищем у:
2х+10у=21
Подставляем найденное значение х
2×3,3+10у=21
6,6+10у=21
10у=21-6,6
10у=14,4
У=14,4 : 10
У=1,44
4) 2х-у=3
х-2,5у=10
Домножаем второй уравнение на ( -2)
2х-у=3
- 2х-5у= -20
Иксы сокращаются , остаётся
6у= -17
У= - 17 : 6
У= - 2,83
Ищем х :
Подставляем найденное значение у в первое уравнение:
2х-(-2,83)=3
2х+2,83=3
2х= 3-2,83
2х=0,17
Х=0,085
5)-
6)-