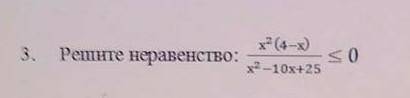
Ньютон на протяжении недели каждое утро садится под яблоню и размышляет. В первый день ему на голову свалилось одно яблоко. Каждый день ему падало на голову на два яблока больше, чем в предыдущий.
Вопрос: сколько шишек будет на голове у Ньютона к концу недели?
Решается суммой арифметической прогрессии.
d = 2 ( потому что каждый день сваливается на два яблока больше, то бишь + 2).
n = 7 (Ньютон ходит к яблоне на протяжении недели раз в день)
a1 = 1 (в первый день стукнуло только одним)
S = n*(2a1 + d(n-1)) /2
S = 7(2*1 + 2*6)/2 = 49
Итого 49 шишек на одну голову (зато на какую!)
Уравнение имеет единственное решение: x = 4
Объяснение:
√(2х+1)+√(х-3)=4+log1/2 (x-3)
ОДЗ: x-3 > 0
Для удобства можно заменить: x-3 = t>0; 2x+1 = 2(t+3)+1 = 2t+7
√(2t+7)+√t - log1/2 t - 4 = 0
√(2t+7)+√t + log2 t - 4 = 0
Заметим, что при t > 0 функции: √(2t+7), √t, log2 t монотонно возрастают, а значит функция f(t) = √(2t+7)+√t + log2 t - 4 также монотонно возрастает. Таким образом, функция f(t) может принимать нулевое значение только в одной точке, иначе говоря, уравнение f(t) = 0 имеет не более одного решения.
Нетрудно заметить, что это решение существует: t = 1
Действительно, подставляя t = 1 в данное уравнение имеем:
√9+√1 + log2 1 - 4 = 0 - верно.
Возвращаемся к замене:
x-3 = 1
x = 4
x²(4 - x)/(x² - 10x + 25) ≤ 0
x²(4 - x)/(x - 5)² ≤ 0
Метод интервалов
[0][4] (5)
x ∈ {0} U [4, 5) U (5, +∞)