решение на фотографии
Объяснение:
м. Крамера: находим 4 определителя.
1: это основная матрица
2: вместо первого столбика пишем числа, не относящиеся к переменным, - это -6, -5 и -2.
3: числа вместо 2 столбика
4: числа вместо 3 столбика
Далее по формулам также ищем значения самих переменных.
м Гаусса: меняются только строки, рядом с которыми написаны действия.
Допустим, 1я матрица, рядом с первой строкой I-III, значит из первой строки вычитаем числа третьей строки. В следующей матрице 1я строка полностью изменила. Где-то мы можем дорожать строки на числа и потом их прибавлять или отнимать, но мы их не меняем в следующей матрице. Должны получится единичная матрица, а числа за чертой, справа, это значения переменных.
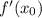производная функции в данной точке. А 
точка касания по иксу.
мы должны найти производную общего типа этой функции.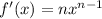
- где n это степень.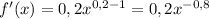
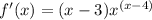
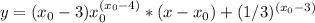
и получаешь уравнение касательной.
Объяснение:
.......................