Для решения этой задачи используем формулы арифметической прогрессии.
а₁=5 [в первый день 5 капель]
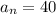 [день, в который нужно выпить 40 капель]
[день, в который нужно выпить 40 капель]
d=5 [разность арифметической прогрессии, т.к. каждый день дозировка увеличивается на одну и ту же величину - 5 капель]
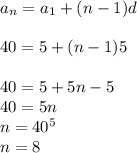
На восьмой день дозировка составит 40 капель.
По формуле суммы n первых членов арифметической прогрессии найдм сколько всего капель нужно выпить больному за 8 дней.
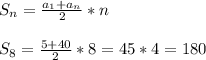
180 капель должен выпить больной за первые 8 дней лечения.
В последний период лечения больной должен уменьшать дозировку каждый день на 5 капель, и с дозировки в 40 капель дойти до 5 капель.
На это ему понадобиться 8 дней (также, как и в первый период лечения).
Суммарное количество капель, которые должен выпить больной за эти 8 дней, составит 180.
В середине лечения больной должен три дня подряд пить по 40 капель. Два раза по 40 капель мы уже учли. Поэтому к общей сумме добавим только 40.
180+180+40 = 400 (капель) - должен выпить больной за весь период лечения.
В одном пузырьке содержится 200 капель лекарства. Значит больному нужно купить 400:200 = 2 пузырька лекарства.
ответ: 2 пузырька.
Пусть за х дней может закончить Катя, тогда еѐ производительность равна / х .
А за у дней может закончить Алиса, тогда еѐ производительность равна / у .
Т.к. они могут напечатать курсовую работу за 6 дней,
то /х + /у = 1/
Если сначала % = / части курсовой напечатает Катя,
а затем завершит работу Алиса, то Алисе остается
% = / части курсовой.
Вся курсовая работа будет выполнена за 12 дней т.е.
( /) х + (/ ) у = .
Решим систему:
/х + /у = / ,
(/) х + (/ ) у = .
+ = ,
+ = ;
у = − , ;
+ * ( − , ) = *( − , )
у = − , ;
, ² − + = ;
у = − , ;
² − + = ;
² − + = ;
= , у =
или = , у = . - не подходит, т.к. Катя печатает быстрее, чем Алиса.
Значит, Катя может напечатать курсовую работу за 10 дней.
ответ. за 10 дней