y=kx+b - уравнение прямой с угловым коэффициентом
Подставим в него координаты точек А и В
А (6;-4)
x=6; y=-4
-4=k·6+b
В (8;4)
x=8; y=4
4=k·8+b
Решаем систему двух уравнений и находим k и b:
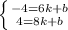
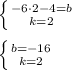
y=2x-16 - уравнение прямой AB с угловым коэффициентом k=2
2x-y-16=0 - общее уравнение прямой АВ
б)
Параллельные прямые имеют одинаковые угловые коэффициенты
y=2x+b - уравнение прямых, параллельных АВ
Чтобы найти прямую, проходящую через точку С подставим координаты точки С
С (-1;6)
6=2·(-1)+b
b=8
y=2x+8 - уравнение прямой, параллельной АВ и проходящей через точку С.
2x-y+8=0 общее уравнение прямой, параллельной АВ и проходящей через точку С.
Произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1)
k₁·k₂=-1
k₁=2
k₂=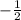
- угловой коэффициент прямой, перпендикулярной АВ
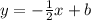- уравнение прямых, перпендикулярных АВ
Подставляем координаты точки С:
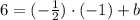
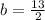
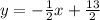-уравнение прямой, перпендикулярной АВ и проходящей через точку С
x+2y-13=0- общее уравнение прямой, перпендикулярной АВ и проходящей через точку С
в)
Прямая, параллельная АВ и проходящей через точку С. пересекается с прямой, перпендикулярной АВ и проходящей через точку С в точке С.
Значит требуется найти точку пересечения прямой АВ и прямой, перпендикулярной АВ и проходящей через точку С
Решаем систему уравнений:
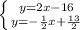
Приравниваем правые части уравнений:
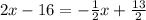
х=9
y=2·9-16
y=2
О т в е т. (9;2)
Если погода поменялась за 3 дня, то возможны варианты:
1) 16 и 17 погода осталась, 18 поменялась. p = 0,7*0,7*0,3 = 0,147
2) 16 осталась, 17 поменялась, 18 осталась. p = 0,7*0,3*0,7 = 0,147
3) 16 поменялась, 17 и 18 осталась. p = 0,3*0,7*0,7 = 0,147
4) 16 поменялась, 17 поменялась, 18 поменялась. p = 0,3*0,3*0,3 = 0,027
Итоговая вероятность равна сумме этих вероятностей
P = 0,147*3 + 0,027 = 0,441 + 0,027 = 0,468
Посчитано без калькулятора!