2) D(y)=(-∞; -6]∪[1; +∞)
3)Смотреть изображение
4)-9; 3
Объяснение:
2) Область определения ф-ции - все значения, которые может принимать независимая переменная (х). Подкоренное выражение корня чётной степени должно быть не меньше нуля, поэтому чтобы найти область определения нужно решить неравенство
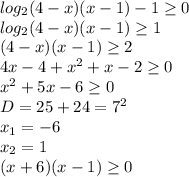
x∈(-∞; -6]∪[1; +∞)
Тогда D(y)=(-∞; -6]∪[1; +∞)
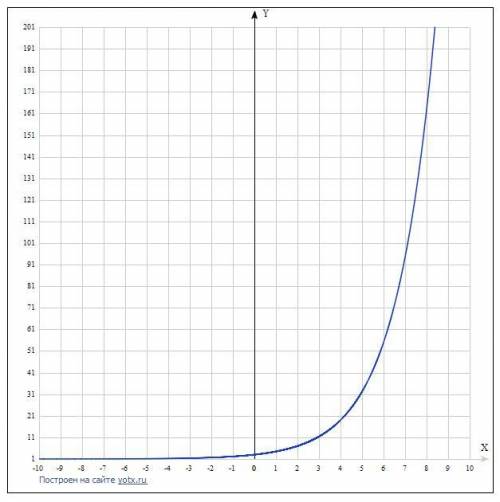
3) Чтобы построить график функции нужно построить график обычной показательной функции без второстепенных коэффициентов. Берём любые значения икса и считаем чему при данных значениях будет равен игрек. Точки с полученными координатами выставляем на координатную плоскость и проводим через эти точки график функции. Потом смещаем график в соответствии с коэффициентами. Свободные коэффициенты указывают на сколько клеток нужно сместить график по ординате. Коэффициент перед иксом Сжимает график по абсциссе обратить внимание, что данная функция является показательной и абсцисса здесь будет являться асимптотой, и график её никогда не пересечёт, хотя будет всё больше и больше приближаться к ней.
4)
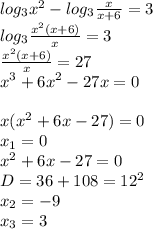
Не забываем про ОДЗ
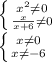
С учётом ОДЗ корень 0 не является корнем уравнения. В ответ идут только -9 и 3
2x≥5 x²-4x+9=0
x≥2.5 D=16-36= -20<0
x∈(-∞; +∞)
x∈[2.5; +∞)
x²-4x+9=(2x-5)²
x²-4x+9=4x²-20x+25
x² -4x² -4x+20x+9-25=0
-3x²+16x-16=0
3x²-16x+16=0
D=(-16)² -4*3*16=256 -192=64
x₁=(16-8)/6=8/6=4/3= 1 ¹/₃∉[2.5; +∞) - не корень уравнения
x₂=(16+8)/6=4
ответ: 4.
2) ОДЗ: 3x+8≥0 x²+3x+6≥0
3x≥ -8 x²+3x+6=0
x≥ - ⁸/₃ D=3² -4*6=9-24=-15<0
x≥ -2 ²/₃ x∈(-∞; +∞)
x∈[-2 ²/₃; +∞)
x²+3x+6=(3x+8)²
x²+3x+6=9x²+48x+64
x²-9x²+3x-48x+6-64=0
-8x²-45x-58=0
8x²+45x+58=0
D=45²-4*8*58=2025-1856=169
x₁=(-45-13)/16=-58/16= -29/8= -3 ⁵/₈∉[-2 ²/₃; +∞) - не корень уравнения
x₂=(-45+13)/16=-32/16= -2
ответ: -2.