Группа точек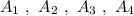 
имеют одинаковую абсциссу х=4 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 
.
.
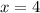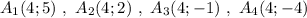Группа точек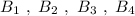 
имеют одинаковую абсциссу х=2 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 
.
.
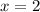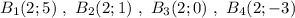Группа точек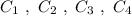 
имеют одинаковую абсциссу х= -2 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 
.
.
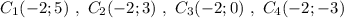Группа точек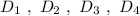 
имеют одинаковую абсциссу х= -4 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 
.
.
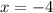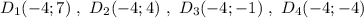Точки, имеющие одинаковую абсциссу, на координатной плоскости лежат на одной прямой, параллельной оси ОУ.
Уравнение такой прямой имеет вид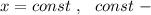 
это число (константа- постоянная величина ) .
Чтобы оценить периметр исходного треугольника, нужно сложить заданные неравенства
2,3 ≤ a ≤ 2,4
3,2 ≤ в ≤ 3,3
4,5 ≤ c ≤ 4,6
2,3+3,2+4,5 ≤ a+в+с ≤ 2,4+3,3+4,6
10 ≤ P ≤ 10,3
Соединили середины сторон, то есть провели 3 средние линии треугольника. Каждая средняя линия равна половине стороны, которой параллельна. Значит, периметр образованного треугольника равен половине периметра исходного треугольника
10 ≤ P ≤ 10,3 | : 2
10:2 ≤ P:2 ≤ 10,3 :2
5 ≤ P₁ ≤ 5,15
ответ : периметр полученного треугольника в пределах от 5 см до 5,15 см включительно.