решить алгебра 7 классса
Задание 2
Найдите значение выражения: 6
,1х8,3 – 0,83=
Задание 3
В таблице представлены цены (в рублях) на некоторые товары в трёх магазинах.
Магазин Хлеб (за батон) Колбаса (за кг) Ветчина (за кг)
«Покупай-ка» 26 370 400
«Свой» 24 360 390
«Мясной ряд» 25 385 410
Марья Ивановна хочет купить 2 батона хлеба, 1 кг колбасы и 0,5 кг ветчины. В каком магазине стоимость такой покупки будет наименьшей, если в «Мясном ряду» у Марьи Ивановны скидка 10% на любые мясные изделия, а в «Покупай-ке» скидка 3% на весь ассортимент?
1) в «Покупай-ке»
2) в «Своём»
3) в «Мясном ряду»
4) во всех магазинах стоимость покупки будет одинаковой
ответ:
Задание 4
Радиолокатор ГИБДД определил, что автомобиль за время, равное 4 с, проехал расстояние 120 м. Выразите скорость автомобиля на этом участке в км/ч?
ответ:
Задание 5
Чашка, которая стоила 90 рублей, продаётся с 10%-й скидкой. При покупке 10 таких чашек покупатель отдал кассиру 1000 рублей. Сколько рублей сдачи он должен получить?
Решение:
ответ:
Задание 6
На заводе производят 120 легковых автомобилей и 60 грузовиков в месяц.
Выберите верные утверждения и запишите в ответе их номера.
1) Завод производит легковых автомобилей не меньше, чем грузовиков.
2) За месяц завод производит в сумме не больше 170 легковых автомобилей и грузовиков.
3) За 2 месяца завод произведет легковых автомобилей ровно в 4 раза больше, чем грузовиков за тот же промежуток времени.
4) За 5 лет завод произведет легковых автомобилей вдвое больше, чем грузовиков
Задание 7
Найдите корень уравнения 8+7Х=9Х+4
Решение:
Задание 8
На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С. Найдите расстояние от точки А до прямой BC. ответ выразите в сантиметрах.
ответ:
Задание 9
В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°, угол ABC равен 106°. Найдите угол ACB.
Решение:
ответ: ( дайте в градусах.)
Задание 10
Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 51 минуту, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 251 км, скорость первого велосипедиста равна 10 км/ч, скорость второго — 20 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи
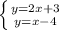 чтобы найти переменную
чтобы найти переменную  , достаточно вычесть от верхней части системы нижнюю, тогда получится
, достаточно вычесть от верхней части системы нижнюю, тогда получится 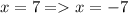 , найдем координату
, найдем координату 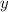 , подставим значение х в любую часть системы:
, подставим значение х в любую часть системы: 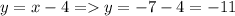 , следовательно точка пересечения этих прямых будет находится по координатам
, следовательно точка пересечения этих прямых будет находится по координатам 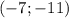
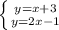
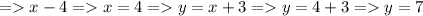 , искомый ответ будет
, искомый ответ будет 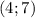
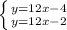 тут возникает противоречие, если прямые вычесть, то мы не сможем найти
тут возникает противоречие, если прямые вычесть, то мы не сможем найти  или
или 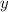 , или же будет
, или же будет 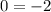 , что не является верным, значит прямые не будут пересекаться, они являются параллельными
, что не является верным, значит прямые не будут пересекаться, они являются параллельными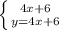 тут уже можно сразу найти
тут уже можно сразу найти  , искомый ответ будет
, искомый ответ будет 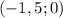
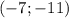 , б)
, б)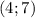 , в)Нет решения, г)
, в)Нет решения, г)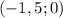
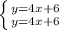 , то это это две прямые, которые совпадают и ответом будет бесконечное множество.
, то это это две прямые, которые совпадают и ответом будет бесконечное множество.
Объяснение:
Линейное уравнение – уравнение, сводящееся к виду ax+b=0, где a≠0,b – числа. Линейное уравнение всегда имеет единственное решение x=−ba. Квадратное уравнение – уравнение, сводящееся к виду ax2+bx+c=0, где a≠0,b,c – числа. Выражение D=b2−4ac называется дискриминантом квадратного уравнения. Квадратное уравнение может иметь не более двух корней: ∙ если D>0, то оно имеет два различных корня и x1=−b+D2aиx2=−b−D2a ∙ если D=0, то оно имеет один корень (иногда говорят, что два совпадающих) x1=x2=−b2a ∙ если D<0, то оно не имеет корней. ▸ Теорема Виета для квадратного уравнения: Если квадратное уравнение имеет неотрицательный дискриминант, то сумма корней уравнения x1+x2=−ba а произведение x1⋅x2=ca ▸ Если квадратное уравнение: ∼ имеет два корня x1 и x2, то ax2+bx+c=a(x−x1)(x−x2). ∼ имеет один корень x1 (иногда говорят, что два совпадающих), то ax2+bx+c=a(x−x1)2. ∼ не имеет корней, то квадратный трехчлен ax2+bc+c никогда не может быть равен нулю. Более того, он при всех x строго одного знака: либо положителен, либо отрицателен. ▸ Полезные формулы сокращенного умножения: x2−y2=(x−y)(x+y)(x+y)2=x2+2xy+y2(x−y)2=x2−2xy+y2 Ознакомиться с полной теорией