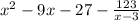
Объяснение:
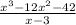
Быстрый и компактный метод для деления многочлена на двучлен вида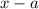 
- схема Горнера: в верхнюю строчку схемы записываются коэффициенты делимого многочлена, снизу записываются коэффициенты многочлена (на степень ниже), который получится в частном. Слева от коэффициентов частного пишут 
:
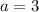| 1 | -12 | 0 | - 42
3 | | | |
Алгоритм следующий: из верхней строчки смещаем в нижнюю первое число, далее умножаем на 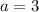и складываем со следующим в верхней строчке числом. И повторяется до конца. Число в последней клетке будет остатком:
| 1 | -12 | 0 | - 42
3 | 1 | -9 |-27| -123
Таким образом,
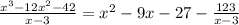
Объяснение:
Пусть за первую книгу заплатили х руб, тогда за вторую заплатили
(360 - х)
Выручка от продажи составила
360 *25% : 100% = 90 рублей
Прибыль с первой книги будет составлять 50% т.е - 0,5х , а
12,5% - 0,125
0,125 * (360 - х) = (45 - 0,125х) - прибыль со второй книги
Уравнение
0,5х + (45 - 0,125х) = 90
0,5х - 0,125х = 90 - 45
0,375х = 45
х = 45 : 0,375
х = 120 руб цена первой книги
360 - 120 = 240 руб - цена второй книги
а) 14а - в ; б) x² + x - 20 ; в) 3x² - x
Объяснение:
а)
1. Раскроем скобки [ 12а-(в-2а) ]
Получаем : 12а - в + 2а
(Когда перед скобками стоит знак "-", измените знак каждого члена в скобках)
2. Приведём подобные члены [ 12а - в + 2а ]
Получаем : 14а - в
ответ : 14а - в
б)
1. Перемножим выражение в скобках [ (х-4) (х+5) ]
Получаем : x * x + 5x - 4x - 4 *5
2. Вычислим произведение [ x * x + 5x - 4x - 4 *5 ]
Получаем : x² + 5x - 4x - 4 * 5
3. Умножаем числа [ x² + 5x - 4x - 4 * 5 ]
Получаем : x² + 5x - 4x - 20
4. Приводим подобные члены [ x² + 5x - 4x - 20 ]
Получаем : x² + x - 20
ответ : x² + x - 20
в)
1. Распределим 2x через скобки [ 2х * (х+1) + х(х-3) ]
Получаем : 2x² + 2x + x * (x - 3)
2. Распределим x через скобки [ 2x² + 2x + x * (x - 3) ]
Получаем : 2x² + 2x + x² - 3x
3. Приводим подобные члены [ 2x² + 2x + x² - 3x ]
Получаем : 3x² + 2x - 3x
4. Приводим подобные члены [ 3x² + 2x - 3x ]
Получаем : 3x² - x
ответ : 3x² - x