![\sqrt[5]{243 \times \frac{1}{32} } = \sqrt[5]{243} \times \sqrt[5]{ \frac{1}{32} } = \\ = \sqrt[5]{ {3}^{5} } \times \sqrt[5]{( \frac{1}{2} ) ^{5} } = 3 \times \frac{1}{2} = \frac{3}{2} = 1.5](/tpl/images/1330/3704/177af.png)
![\sqrt[3]{ \frac{8}{125} } = \frac{ \sqrt[3]{8} }{ \sqrt[3]{125} } = \frac{ \sqrt[3]{2^{3} } }{ \sqrt[3]{ {5}^{3} } } = \frac{2}{5} = 0.4 \\](/tpl/images/1330/3704/31221.png)
![\sqrt[6]{64 \times \frac{1}{729} } = \sqrt[6]{64} \times \sqrt[6]{ \frac{1}{729} } = \\ = \sqrt[6]{ {2}^{6} } \times \sqrt[6]{( \frac{1}{3} )^{6} } = 2 \times \frac{1}{3} = \frac{2}{3}](/tpl/images/1330/3704/97250.png)
![\sqrt[5]{ - 7 \frac{19}{32} } = \sqrt[5]{ - \frac{243}{32} } = \\ = - \frac{ \sqrt[5]{ {3}^{5} } }{ \sqrt[5]{ {2}^{5} } } = - \frac{3}{2} = - 1. 5](/tpl/images/1330/3704/770c3.png)
48 квадратных сантиметров
Объяснение:
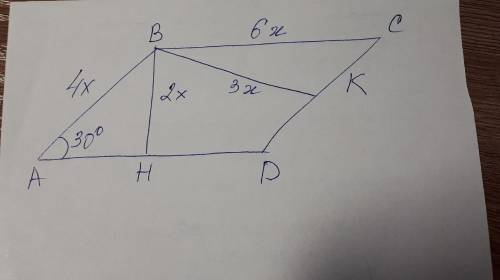
1) Примем одну высоту параллелограмма за 2х (на рисунке это сторона BH), тогда вторую высоту примем за 3х (на рисунке это сторона BK).
2) Поскольку катет против угла в 30° равен половине гипотенузы, то из треугольника АВН получаем, что гипотенуза АВ = 4х.
3) Далее рассмотрим треугольник ВСК. Получаем, что сторона ВС= 6х
4) Затем вычислим периметр параллелограмма: (4х+6х)*2=40 сантиметров
5) 20х=40, откуда х=2
6) Таким образом, можно сделать вывод, что одна сторона 4х=4·2=8 см.
7) Высота проведенная к этой стороне 3х=3·2=6 см
8) Таким образом получаем, что площадь параллелограмма равна 8*6=48 квадратных сантиметров
Если ветви параболы направлены вниз, то квадратичная функция у=ах²+bx+c в вершине параболы принимает наибольшее значение и коэффициент при х² меньше 0, то есть а<0.
Координаты вершины х(верш)= -b/2a
y(верш)=ах²(верш)+bx(верш)+с=a(-b/2a)²+b(-b/2a)+c
x(верш)=-(а-3)/2а
а(а-3)² (а-3)² (а-3)² (а-3)²
у(верш)= - +1=4 , - - 3=0 ,
4а² 2а 4а 2а
а²-6а+9-2(а²-6а+9)-12а
=0
4а
-а²+6а-9-12а=0
-а²-6а-9=0 , а²+6а+9=0 , (а+3)²=0 , а=-3