Определить промежутки монотонности функции, не используя производную функции.
y = (x² - x - 20)² - 18
=================================
Область определения функции D (y) = R
y = (x² - x - 20)² - 18
Квадратичная функция в квадратичной функции
y = f(z); z = g(x)
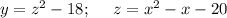
Чтобы найти промежутки монотонности квадратичной функции, нужно найти абсциссу вершины параболы.
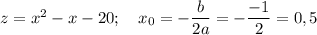 - координата вершины
- координата вершины
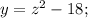 z = 0 - координата вершины параболы
z = 0 - координата вершины параболы

x₁ = -4; x₂ = 5 - координаты вершин параболы
Таким образом, есть три точки, которые определяют промежутки монотонности функции y = (x² - x - 20)² - 18.
x₁ = -4; x₀ = 0,5; x₂ = 5
x ∈ (-∞; -4] - функция убывает : y(-5) > y(-4)
x ∈ [-4; 0,5] - функция возрастает : y(-4) < y(0)
x ∈ [0,5; 5] - функция убывает : y(1) > y(2)
x ∈ [5; +∞) - функция возрастает : y(5) < y(6)
Y = 5cosx - 12sinx - 8
1)5cosx-12sinx
Введем дополнительный угол:
√(5²+12²) = √25+144 = √169 = 13
5cosx-12sinx = 13(5/13cosx - 12/13sinx) = 13cos(x+arccos(5/13))
2)-1 <= cos(x+arccos(5/13)) <= 1|•13
-13 <= 13cos(x+arccos (5/13)) <= 13|-8
-21 <= 13cos(x+arccos(5/13))-8 <= 5
ответ: [-21; 5]