1) Формула с номером 3 - y-y0=k(x-x0) - раскрывает геометрический смысл производной. Эта формула говорит нам о том, что производная функции в точке (x0, y0) равна тангенсу угла наклона касательной, проведенной к графику функции в этой точке.
2) Для вычисления (6x^3)' мы применяем правило дифференцирования степенной функции. Умножаем показатель степени на коэффициент перед переменной и затем уменьшаем показатель степени на 1. В данном случае получаем 3 * 6 * x^(3-1) = 18x^2, поэтому правильный ответ - 3) 18x^2.
3) Вычисления ()' осуществляются аналогично предыдущему вопросу. Исходя из формулы, (х^2)' = 2x, поэтому правильный ответ - 2) 2x.
4) Формула, задающая (u·v)', - 4) u'·v + u·v'. Это следует из правила дифференцирования произведения функций. При дифференцировании (u·v) с помощью этой формулы, сначала находим производную первой функции u и домножаем ее на v, затем находим производную второй функции v и домножаем ее на u.
5) Чтобы вычислить ((x-1)^5)', мы снова используем правило дифференцирования степенной функции и применяем его ко всем членам многочлена, используя формулу (x^n)' = n * x^(n-1). В данном случае получаем 5 * (x-1)^(5-1) = 5 * (x-1)^4, поэтому правильный ответ - 2) 5(x-1)^4.
6) Чтобы найти производную функции f(x) = 2x^2 - 3x + 1 в точке x0=1, мы сначала дифференцируем каждый член по отдельности, применяя правила дифференцирования степенных функций и констант. Получаем f'(x) = 4x - 3. Затем подставляем x=1 в полученную производную, получаем f'(1) = 4(1) - 3 = 4 - 3 = 1, поэтому правильный ответ - 1) 1.
7) Для вычисления (x^3 + 2x^4 - x)' мы снова дифференцируем каждый член по отдельности, используя правила дифференцирования степенных функций. Получаем (3x^2) + (2 * 4x^3) - 1 = 3x^2 + 8x^3 - x, поэтому правильный ответ - 2) 3x^2 + 8x^3 - x^2.
8) Чтобы найти производную функции y = x · ?, мы дифференцируем каждый член функции. Поскольку ?, это функция, которая не определена в вопросе, затрудняюсь дать точный ответ.
9) Аналогично предыдущему вопросу, чтобы найти производную функции y = x^5 - ?, мы дифференцируем каждый член функции. Поскольку ?, это функция, которая не определена в вопросе, затрудняюсь дать точный ответ.
10) Найти производную функции y = ? не имеет смысла, поскольку ?, это функция, которая не определена в вопросе.
11) Найдите производную функции y = 1. Поскольку константа взята в качестве функции, ее производная всегда равна нулю, поэтому правильный ответ - 2) 0.
12) Чтобы найти производную функции y = ?, мы дифференцируем каждый член функции. Поскольку ?, это функция, которая не определена в вопросе, затрудняюсь дать точный ответ.
13) Для вычисления (2x^10 - 3x^5 + 3)', мы дифференцируем каждый член функции, используя правила дифференцирования степенных функций. Получаем 20x^9 - 15x^4, поэтому правильный ответ - 4) 20x^9 - 15x^4.
14) Формула, задающая ?, - 4) u' - u. Это следует из правила дифференцирования разности функций. При дифференцировании (u - v) с помощью этой формулы, сначала находим производную первой функции u, затем находим производную второй функции v и вычитаем ее из производной первой функции u.
15) Формула с номером 3 - (t) = S'(t) - раскрывает механический смысл производной. Эта формула говорит нам о том, что производная функции S(t) является скоростью изменения зависимой переменной (пути, объема, температуры и т.д.) относительно независимой переменной (времени, объема, температуры и т.д.).
Хорошо, давайте рассмотрим каждую задачу по очереди.
1) Вероятность вытащить первую конфету "Аленка" из мешка составляет 30/80, так как в мешке находится 30 "Аленок" и 80 конфет в общей сложности. После вытаскивания первой конфеты в мешке остается 79 конфет, из которых 49 "Белочек". Таким образом, вероятность вытащить вторую конфету "Белочка" составляет 49/79. После вытаскивания второй конфеты в мешке остается 78 конфет, из которых 48 "Белочек". Таким образом, вероятность вытащить третью конфету "Белочка" составляет 48/78.
Для определения вероятности получения конфет в указанной последовательности, мы должны перемножить вероятности каждого события:
(30/80) * (49/79) * (48/78) = 0.0725
Таким образом, вероятность того, что первые три ребенка получат конфеты в последовательности "Аленка" - "Белочка" - "Белочка", составляет 0.0725 или 7.25%.
2) В данном случае в урне находятся 6 карточек с буквами "п", "о", "б", "е", "д" и "а". Нам необходимо вытащить 4 карточки и сформировать слово "обед" или "беда".
Сначала рассмотрим возможность составления слова "обед". Вероятность вытащить букву "о" равна 1/6, так как в урне находится одна карточка с этой буквой. После вытащивши букву "о", в урне остается 5 карточек, из которых 1 "б", 2 "е", 1 "д" и 1 "а". Таким образом, вероятность вытащить букву "б" равна 1/5. После этого остается 4 карточки с вероятностью 2 "е"/4, 1 "д"/3 и 1 "а"/2.
Теперь посчитаем вероятность получения слова "беда". Вероятность вытащить букву "б" равна 1/6, так как в урне находится одна карточка с этой буквой. После этого остается 5 карточек с вероятностью 1 "о"/5, 2 "е"/4, 1 "д"/3 и 1 "а"/2.
Чтобы получить итоговую вероятность, мы должны применить теорему о сложении для составления слова "обед" и слова "беда". Таким образом, вероятность получения либо слова "обед", либо слова "беда" составляет:
(1/6 * 2/5 * 2/4 * 1/3) + (1/6 * 1/5 * 2/4 * 1/3) = 0.0333 + 0.0111 = 0.0444
Таким образом, вероятность выигрыша в данной игре составляет 0.0444 или 4.44%.
Знаменатель не равен нулю, значит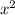 + х-2≠0
+ х-2≠0
(x+2)(x-1)≠0
x≠ - 2 и x≠1
Значит
(х-2)(х-1)=0
х=2 и х=1
Но х≠1,
ответ: х=2