В решении.
Объяснение:
220.
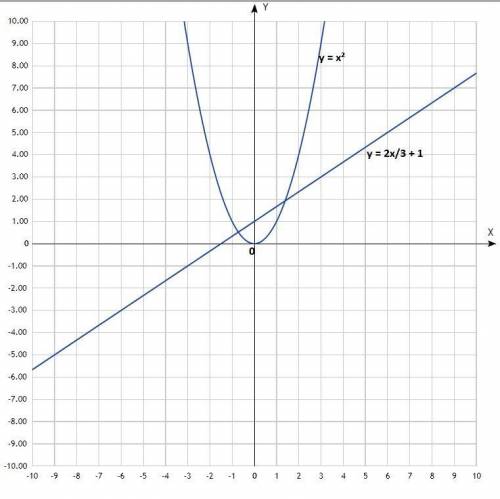
1) Построить графики: у = х²; 2х - 3у + 3 = 0.
Первый - классическая парабола, второй - прямая линия.
Преобразовать второе уравнение в уравнение функции:
2х - 3у + 3 = 0;
-3у = -2х - 3
3у = 2х + 3
у = (2х + 3)/3
у = 2х/3 + 1;
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = х²; у = 2х/3 + 1;
Таблицы:
х -3 -2 -1 0 1 2 3 х -3 0 3
у 9 4 1 0 1 4 9 у -1 1 3
По вычисленным точкам построить графики.
Согласно рисунка, координаты точек пересечения графиков:
(-0,7; 0,5); (1,4; 1,9).
2)
а) Решить графически систему уравнений:
у = х²
2х - 3у + 3 = 0
Графическое решение в 1).
Решения системы уравнений: (-0,7; 0,5); (1,4; 1,9).
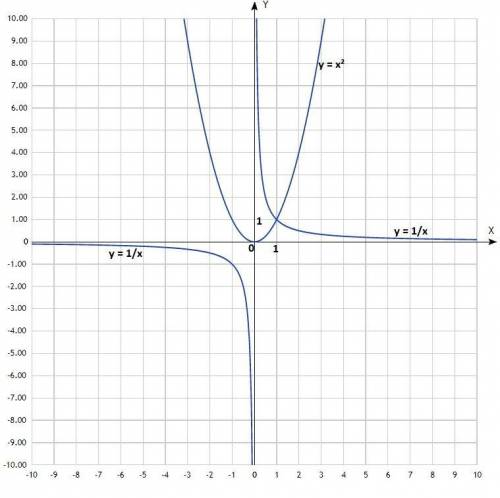
б) у = х²;
у = 1/х;
Построить графики. Первый - классическая парабола, второй - гипербола.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = х²; у = 1/х;
Таблицы:
х -3 -2 -1 0 1 2 3 х -10 -5 -2 -1 0 1 2 5 10
у 9 4 1 0 1 4 9 у -0,1 -0,2 -0,5 -1 - 1 0,5 0,2 0,1
По вычисленным точкам построить графики.
Согласно рисунка, координаты точки пересечения графиков: (1; 1).
Решение системы уравнений: (1; 1).
1)129
Объяснение:
3)Найдем значение данного выражения (-3,25 - 2,75) : (-0,6) + 0,8 * (-7) по действиям (сначала разность в скобках, затем деление, далее произведение и сумма): 1) -3,25 - 2,75 = (складываем числа по модулю и в ответе ставим знак "минус") = -6; 2) -6 : (- 0,6) = (делим по модулю и в ответе ставим знак "плюс") = 10; 3) 0,8 * (-7) = (умножаем числа по модулю и в ответе ставим знак "минус") = -5,6; 4) 10 + (-5,6) = (от модуля большего числа отнимаем модуль меньшего числа и ставим знак модуля большего числа) = 4,4. ответ: 4,4.