Не понятно чему равна первая функция, поэтому напишу просто как решить. Если графики функций пересекаются значит у них обоих имеется одна и таже общая точка, т.е.координаты этой точки удовлетворяют обоим уравнениям. Теперь чтобы найти эту точку делаем следующее: из любого уравнения выражаем какую-либо неизвестную через другую, н-р, я выражу из второго уравнения х. 3x+5y=-12
3х=-12-5у
х=(-12-5у)/3
Затем в другое уравнение вместо х подставляем полученное выражение
2( (-12-5у)/3 )-3y = (тут уж я не знаю чему там у тебя равно) Преобразуем выражение и находим у
(-24-10у)/3 - 3у= (дальше я преобразовать не могу так не знаю числа стоящего после равно)
Нашли у ( должно получиться какое-нибудь число)
Полученное число нужно подставить в выделенное выражение и получим х. Данные два числа записываем как координаты точки (х,у)
На складе стеклотары хранятся банки емкостью 0,5 л, 0,7 л и 1 л. Сейчас на складе 2500 банок общей емкостью 2000 л. Докажите, что на складе есть хотя бы одна 0,5 литровая банка.
Пусть банки по 0.5 л - x; по 0.7 л - y; по 1 л - z. Составим систему уравнений:
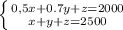
Допустим, что банки по 0.5л отсутствуют. Тогда x = 0. Попробуем решить систему:
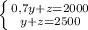
Умножаем второе уравнение на 0,7:
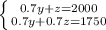
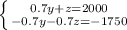
0.3z=250
z = 250 : 0,3
Целочисленного решения данной системы не существует. Учитывая, что 1 банка = 1 единице утверждение отсутствия банок емкостью 0.5 л ложно! А значит, есть хотя бы одна 0.5 литровая банка.
Ч.Т.Д
y=0
Объяснение: