4 км/час и 6 км/час
Объяснение:
пусть х км/час - скорость 1- го пешехода( х>0),
у км /час-скорость 2-го пешехода у>0)
(12/х) час-время в пути первого пешехода до встречи,
(12/ у) час-время в пути 2-го пешехода до встречи
по условию задачи известно, что первый был в пути на 1 час больше(в условии сказано, что один из них вышел на один час раньше второго. я выбрала , что это первый пешеход)
уравнение:
(12/ х)-(12/у)=1
по условию известно, что если бы пешеходы вышли одновременно, то встретились бы через 2 часа 24 минуты (144/60 час), тогда (х+у) км/час - скорость сближения
уравнение:
(х+у)*(144/60)=24
система уравнений:
решить систему уравнений, получим х=4 км/час
у=6 км/час
Объяснение:
Объяснение:
Данная функция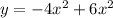 является квадратичной функцией (многочлен второй степени) и задаёт квадратичную параболу. Как известно, у такой функции может быть лишь один экстремум, находящийся в вершине параболы.
является квадратичной функцией (многочлен второй степени) и задаёт квадратичную параболу. Как известно, у такой функции может быть лишь один экстремум, находящийся в вершине параболы.
Упростим исходную функцию: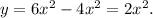
Для нахождения единственного экстремума воспользуемся производной:
единственного экстремума воспользуемся производной: 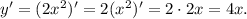
По лемме Ферма, значение производной от экстремума нулевое. Таким образом,
экстремума нулевое. Таким образом,  точки экстремума будет решением
точки экстремума будет решением 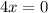 .
.
Для нахождения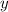 точки экстремума вычислим значение исходной функции от найденного
точки экстремума вычислим значение исходной функции от найденного  :
:
Получается, что координаты точки экстремума это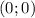 .
.