Заметим, что . Пусть . Тогда из первой строки получим, что . Подставив это во вторую строку системы, получим . Тогда получим систему, которая будет состоять из строк и . Решая две полученные системы уравнений, находим, что исходная система уравнений имеет две пары решений вида . Тогда окончательным ответом с учетом ОДЗ будет: или .
Система уравнений решена!
Комментарий-1:
При решении несложно было заметить, что из второй строки системы следует, что y=5x.
Комментарий-2:
При выполнении замены, можно было указать, что 6x+y=t и проделать аналогичную в решении работу.
При x < -2 будет |x-1| = 1 - x; |x+2| = -x - 2 y = |x-1| - |x+2| = 1 - x - (-x - 2) = 1 - x + x + 2 = 3 При -2 <= x < 1 будет |x+2| = x + 2; |x-1| = 1 - x y = 1 - x - (x + 2) = 1 - 2x - 2 = -2x - 1 При x >= 1 будет |x-1| = x - 1; |x+2| = x + 2 y = x - 1 - (x + 2) = x - 1 - x - 2 = -3 Получается: при x < -2 y = 3; при -2 <= x < 1 y = -2x - 1; при x >= 1 y = -3 При k >= 0 прямая пересекается в 1 точке. При -2 < k < 0 прямая пересекается с графиком в 3 точках. При k = -2 прямая совпадает с частью графика на промежутке [-2; 1]. При k < -2 прямая опять пересекается с графиком в 1 точке.
(см. объяснение)
Объяснение:
Заметим, что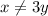
. Пусть 
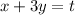. Тогда из первой строки получим, что 
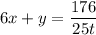. Подставив это во вторую строку системы, получим 
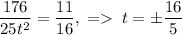. Тогда получим систему, которая будет состоять из строк 
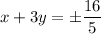и 
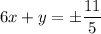. Решая две полученные системы уравнений, находим, что исходная система уравнений имеет две пары решений вида 
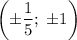. Тогда окончательным ответом с учетом ОДЗ будет: 
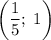или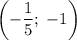 
.
Система уравнений решена!
Комментарий-1:
При решении несложно было заметить, что из второй строки системы следует, что y=5x.
Комментарий-2:
При выполнении замены, можно было указать, что 6x+y=t и проделать аналогичную в решении работу.