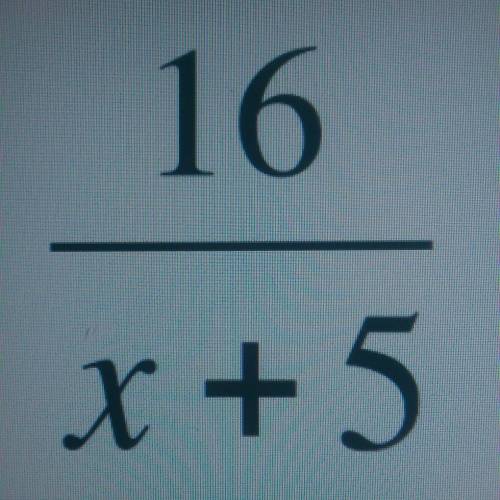
x2 + 4x + 8 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = 42 - 4·1·8 = 16 - 32 = -16
Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.
4x2 - 12x + 9 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = (-12)2 - 4·4·9 = 144 - 144 = 0
Так как дискриминант равен нулю то, квадратное уравнение имеет один действительных корень:
x = 122·4 = 1.5
3x2 - 4x - 1 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = (-4)2 - 4·3·(-1) = 16 + 12 = 28
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = 4 - √282·3 = 23 - 13√7 ≈ -0.21525043702153024
x2 = 4 + √282·3 = 23 + 13√7 ≈ 1.5485837703548635
2x2 - 9x + 15 = 0 Найдем дискриминант квадратного уравнения: D = b2 - 4ac = (-9)2 - 4·2·15 = 81 - 120 = -39 Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.Объяснение:
выражение в квадратном корне должно давать положительный результат, иначе выражение не
имеет смысла
1) √х. х не должен быть –1 или каким-то другим отрицательным числом, поэтому выражение имеет смысл при х (0; +∞)
2) √х². Здесь х также может быть и отрицательным, поскольку он возведён во вторую степень, которая даёт положительный результат в любом случае поэтому: х (–∞; +∞)
3) √–х. х не должен быть положительным, поскольку при положительном х у нас получится отрицательный итог, например при х=1 =√–1, это недопустимо, поэтому х должен быть: х≤0 и значение следующие: х (–∞; 0)
5) √25х. х должен быть 0 или положительное значение:
х≥0, поэтому х (0; +∞)
4) √–3х. х должен быть отрицательным, чтобы выражение давало положительный результат:
х (–∞; –1)
6) √0,01х, х≥0; х (0; +∞)
7)
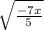
х ≥ 0; х (–∞; 0)
8)
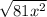
х может быть как положительным так и отрицательным, поскольку он возведён во вторую степень и значение выражения всегда будет положительным: х (–∞; +∞)
Відповідь:
x∈R\{-5}
Пояснення:
x+5≠0
x≠-5
область визначення функції:
x∈R\{-5}