 см, тогда второй катет -
см, тогда второй катет - 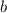 см. Площадь прямоугольного треугольника равна
см. Площадь прямоугольного треугольника равна 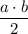 , что составляет 210 см² или перепишем сразу
, что составляет 210 см² или перепишем сразу 
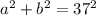
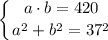
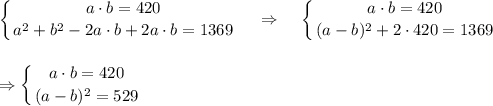
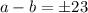 . Тогда имеем несколько случаев.
. Тогда имеем несколько случаев. , то
, то 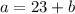 и подставим в первое уравнение.
и подставим в первое уравнение.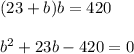
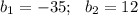 см и корень
см и корень 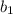 не удовлетворяет заданному условию
не удовлетворяет заданному условию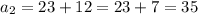 см
см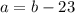 ,то подставив в первое уравнение, получим
,то подставив в первое уравнение, получим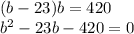
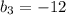
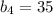 см и корень
см и корень 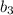 не удовлетворяет условию
не удовлетворяет условию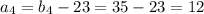
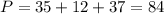 см
см
Решение системы уравнений (-4 и 4/9; 9 и 1/3), или (-40/9; 28/3).
Объяснение:
Решить систему уравнений
x/4+y/3=2
x/2-y/12= -3
Умножить оба уравнения на 12, чтобы избавиться от дроби:
3х+4у=24
6х-у= -36
Выразим у через х во втором уравнении, подставим выражение в первое уравнение и вычислим х:
-у= -36-6х
у=36+6х
3х+4(36+6х)=24
3х+144+24х=24
27х=24-144
27х= -120
х= -120/27
х= -4 и 4/9
у=36+6х
у=36+6*(-4 и 4/9)
у=9 и 1/3
Решение системы уравнений (-4 и 4/9; 9 и 1/3), или (-40/9; 28/3).