9
Объяснение:
Раскрывваем скобки:
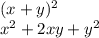
Подставляем х = 2, у = 1, тогда:
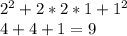
cамый легкий здесь - использование формул сокращенного умножения. так (х²+1)²=х⁴+2х²+1, поэтому, если представить, что
х²=2х²-х², то легко выйти на формулу разности квадратов, итак,
х⁴+х²+1 =(х⁴+2х²+1) -х²=(х²+1)²-х²=(х²+1-х)(х²+1+х), конечно, можно продолжать раскладывать каждый квадратный трехчлен на множители, но уже не на действительные, т.к. у каждой скобки дискриминант меньше нуля, и действительных корней не получим. итак, если необходимо продолжить, то
х²+1-х=0; х=(1±√(1-4))/2=(1±√3i)/2, и тогда (х²+1-х)=(х-(1+√3i)/2)((х-(1-√3i)/2);
аналогично х²+1+х=0; х=(-1±√(1-4))/2=(1±√3i)/2, и тогда (х²+1+х)=
(х-(-1+√3i)/2)((х-(-1-√3i)/2);
и разложение можно продолжить.
х⁴+х²+1 =(х-(1+√3i)/2)((х-(1-√3i)/2)(х-(-1+√3i)/2)((х-(-1-√3i)/2);
cамый легкий здесь - использование формул сокращенного умножения. так (х²+1)²=х⁴+2х²+1, поэтому, если представить, что
х²=2х²-х², то легко выйти на формулу разности квадратов, итак,
х⁴+х²+1 =(х⁴+2х²+1) -х²=(х²+1)²-х²=(х²+1-х)(х²+1+х), конечно, можно продолжать раскладывать каждый квадратный трехчлен на множители, но уже не на действительные, т.к. у каждой скобки дискриминант меньше нуля, и действительных корней не получим. итак, если необходимо продолжить, то
х²+1-х=0; х=(1±√(1-4))/2=(1±√3i)/2, и тогда (х²+1-х)=(х-(1+√3i)/2)((х-(1-√3i)/2);
аналогично х²+1+х=0; х=(-1±√(1-4))/2=(1±√3i)/2, и тогда (х²+1+х)=
(х-(-1+√3i)/2)((х-(-1-√3i)/2);
и разложение можно продолжить.
х⁴+х²+1 =(х-(1+√3i)/2)((х-(1-√3i)/2)(х-(-1+√3i)/2)((х-(-1-√3i)/2);
9
Объяснение:
раскладываем на x2 + 2xy + y2
подставляем свои значения 4 + 4 + 1=9