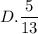
Объяснение:
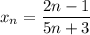
Если
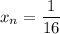 , то
, то
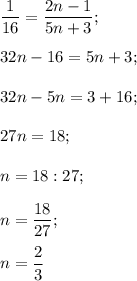
Так как полученное число n не является натуральным числом, то число 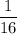 не является членом последовательности.
не является членом последовательности.
Если 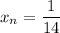 , то
, то
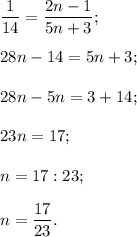
Так как полученное число n не является натуральным числом, то число
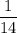 не является членом последовательности.
не является членом последовательности.
Если  , то
, то
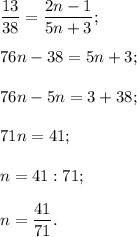
Так как полученное число n не является натуральным числом, то число
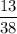 не является членом последовательности.
не является членом последовательности.
Если 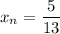 , то
, то
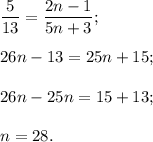
Так как полученное число n является натуральным числом, то число
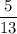 является 28 членом данной последовательности.
является 28 членом данной последовательности.
Если 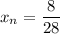 , то
, то
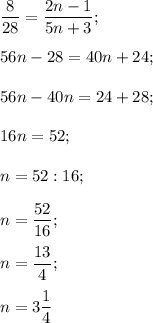
Так как полученное число n не является натуральным числом, то число
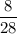 не является членом последовательности.
не является членом последовательности.
Тогда верный ответ: 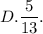
ответ: 6 множеств
Объяснение:
1. Покажем, что наше множество не может содержать более 2 элементов. В самом деле, если множество содержит три элемента, то после упорядочивания по возрастанию получим:
a<b<c,
причём по условию ab=bc, отсюда a=c, что невозможно ввиду неравенства a<c. Если же множество содержит не менее четырёх элементов, то выделим в нём два наименьших и два наибольших, тогда после упорядочивания по возрастанию получим:
a<b<…<c<d,
причём ab=cd, но такое равенство невозможно, поскольку a<c и b<d. Следовательно, наше множество содержит 2 элемента.
2. Таким образом, задача свелась к подсчёту числа решений уравнения:
ab=2020, a<b.
Поскольку 2020 не является полным квадратом, то это число есть в точности половина делителей числа 2020, то есть 6.
ответ: 18,620976
Объяснение:
1) 21/3=7
2) 7*41=287
3) 287/2=143,5
4) 2,5*21=52,5
5) 52,5/2=26,25
6) 143,5-26,25=117,25
7) 45,09/1,5=30,06
8) 41/4=10,25
9) 117,25/10,25=11,439024...
10) 30,06-11,439024=18,620976