Проведем отрезки OB и OC, как показано на рисунке. Расстоянием от точки до прямой является длина перпендикуляра, проведенного к прямой. Поэтому, OE перпендикулярен AB, а OF перпендикулярен CD. Точки E и F делят свои хорды пополам (по свойству хорды) Получается, что треугольники OEB и OCF - прямоугольные, EB=AB/2 и CF=CD/2. По теореме Пифагора: OB2=OE2+EB2 OB2=242+(20/2)2 OB2=576+100=676 OB=26 OB=OC=26 (т.к. OB и OC - радиусы окружности) По теореме Пифагора: OC2=CF2+FO2 OC2=(CD/2)2+FO2 262=(CD/2)2+102 676=(CD/2)2+100 (CD/2)2=576 CD/2=24 CD=48 ответ: CD=48
Неполным квадратным называется такое уравнение,в котором хотя бы один из коэффициентов, кроме старшего( либо второй, либо свободный член) равен нулю. В нашем уравнении: b= -(a-6); c=(a^2-9). Старший коэффициент "a" = (a+3). Он не должен равняться нулю ( при а=-3), т.к. уравнение уже не будет квадратным. Поэтому,а=-3 нас не устраивает. 1). b=0 a-6=0 a=6 2)c=0 a^2-9=0 a^2=9 a1=-3 ( нам не подходит этот вариант) a2=3 При а =3 уравнение выглядит так: 6x^2+3x=0 При а=6 уравнение выглядит так:9x^2+27=0 ответ: a=3; a=6
Окей.
1) x²-10x+25 = 0
a=1 b=-10 c=25
D = b²-4ac => (-10²)-4*1*25 = 100-100 = 0=0, 1 корень
x =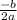
x₁ =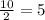
ответ: корень 5.
2)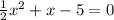
0,5x^2+x-5=0
a=0,5 b=1 c=-5
D = b²-4ac => 1²-4*0,5*(-5) = 1+10 = 11>0, 2 корня
x =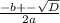
x₁ =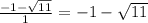
x₂ =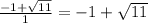
ответ: 1) -1 - √11; 2) -1 + √11.