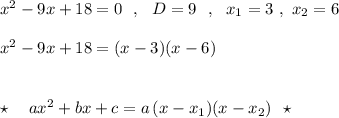
Розкладіть на лінійні множники квадратний тричлен х²- 9x + 18
Разложить на линейные множители квадратный трехчлен х²- 9x + 18
ax²+bx +c = a(x -x₁)(x -x₂), где x₁ и x₂ корни трехчлена
х²- 9x + 18 =0 ⇔х²- (3+6)x + 3*8 =0 ⇒ x₁=3 и x₂= 6 т. Виета
х²- 9x + 18 = (x - 3) (x - 6)
Решите уравнение
(X+1)^2/3-(X-1)/2=(8X-1)/6
(X+1)^2/3-(X-1)/2=(8X-1)/6 |*6
2(X+1)^2-3(X-1)=8X-1
2x^2+4x+2-3x+3-8x+1=0
2x^2-7x+6=0
D=49-4*2*6=1
x=1,5
x=2
Решите уравнение
(2X-3)^2-2(5X-4)(X+1)=-9-13X
(2X-3)^2-2(5X-4)(X+1)=-9-13X
4x^2-12x+9-2(5x^2+5x-4x-4)+9+13x=0
4x^2-12x+9-10x^2-10x+8x+8+9+13x=0
6x^2+x-26=0
D=1-4*6*(-26)=625
x=-13/6
x=2
Не вычисляя корней квадратного уравнения, решите уравнение
1) 3X^2-2X-6=0
y(первое)=3X^2-2X-6
y(второе)=0
найдем координаты вершины параболы:
x(в)=-b/2a=2/6=1/3
y(в)=3(1/3)^2-2(1/3)-6=-19/3
координаты:(-19/3)
8. 1-Б; 2-Г; 3-А; 4-В.
9. 1-Д; 2-Б; 3-Г; 4-А.
Подробнее объяснение:
8. 1) 2cosx = 1
cosx = 1/2
x = ± arccos1/2 + 2πn, n є Z
x = ± π/3 + 2πn, n є Z. Б.
2) 2cosx/2 = 1
cosx/2 = 1/2
x/2 = ± arccos1/2 + 2πn, n є Z
x/2 = ± π/3 + 2πn, n є Z.
x = ± 2π/3 + 4πn, n є Z. Г.
3) cos2x = 1
2x = ± arccos1/2 + 2πn, n є Z
2x = ± π/3 + 2πn, n є Z.
x = ± π/6 + πn, n є Z. А.
4) cosx/2 = 1
x/2 = 2πn, n є Z.
x = 4πn, n є Z. В.
Відповідь: 1-Б; 2-Г; 3-А; 4-В.
9. 1) sin2x = 0. [0; 2π] sinx є [-1; 1]
2x = πn, n є Z
x = πn/2, n є Z n = 0, x = 0 +
n = 1, x = π/2. +
n = 2, x = π +
n = 3, x = 3π/2 +
n = 4, x = 2π. +
n = 5, x = 5π/2 -
П'ять коренів. Д.
2) sin2x = 1. [0; 2π]
2x = π/2 + 2πk, k є Z.
x = π/4 + πk, k є Z.
k = 0, x = π/4. +
k = 1, x = 5π/4. +
k = 2, x = 9π/4. -
Два корені. Б.
3) cos2x = 0. [0; 2π]
2x = π/2 + πm, m є Z.
x = π/4 + πm/2, m є Z.
m = 0, x = π/4. +
m = 1, x = 3π/4. +
m = 2, x = 5π/4. +
m = 3, x = 7π/4. +
m = 4, x = 9π/4. -
Чотири корені. Г.
4) tgx/2 = 1. [0; 2π]
x/2 = arctg1 + πt, t є Z.
x/2 = π/4 + πt, t є Z.
x = π/2 + 2πt, t є Z.
t = 0, x = π/2 . +
t = 1, x = 5π/2. -
Один корінь. А.
Відповідь: 1-Д; 2-Б; 3-Г; 4-А.