Объяснение:
Принимаем всю работу за единицу (1). ⇒
Скорость выполнения работы одним мастером равна 1/12.
Скорость выполнения работы тремя мастерами равна 3/12=1/4.
Скорость выполнения работы одним учеником равна 1/30.
Скорость выполнения работы учеников впятером равна 5/30=1/6. ⇒
Скорость выполнения работы, когда работают 3 мастера и 5 учеников
одновременно равна:
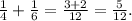
Таким образом, 3 мастера и 5 учеников работая вместе, выполнят работу за: 1:(5/12)=12/5=2,4 (дня).
ответ: 3 мастера и 5 учеников работая вместе,
выполнят работу за 2,4 дня.
ответ ответ дан Solnishkosandra
№1.
а) 1. введу функцию у=3х^2 - 5х - 22.
2. Найду нули фунции через дискриминант:
D= 25 - 4 * 3 * (-22) = 25 + 264 = 289 , Д больше 0, 2 корня.
х1 = ( 5 - 17) / 6 = - 2; х2 = ( 5+ 17) / 6 = 3,7.
3. так как ветви параболы аправленны вверх, решение находится за корнями, то есть х принадлежит ( - бесконечность ; -2) ( 3, 7 ; + бесконечность)
в) 1. 2x^2 + 3х+ 8 = 0
2. D=9 - 4 * 2 * 8 = - 55. Д меньше 0, ветви параболы напр ввер, уравнение решения не имеет.
б) 1. х^2 = 81
х1 = 9, х2 = -9
2. так как ветви параболы направленны вверх, решение находится между корнями. то есть ответ: х принадлежит ( - 9; 9)
№2.
1.нули функции
х1=4, х2 = 1, х3= - 5
2. наносим значения на числовую прямую и
расставляем знаки
- + - +
(-5)(1)(4)> х
3. так как f(x) < 0 (по условию), то выбмраем интервалы, где знак (-), то есть ответ : х принадлежит ( - бесконечность; -5) , (1; 4)
№3
1. Введу ф-цию : 5x^2 + nx +20 = 0
2. D = n^2 - 4 * 5 * 20 = n^2 - 400.
3. Чтобы уравнение не имело корней, D должен быть меньше 0 ( так как при D<0 уравнение не имеет корней) Значит,
n^2 - 400 < 0
n^2 = 400
n1 = 20, n2 = - 20.
ответ: 20, - 20.
1) Пусть S - расстояние между пунктами А и В, скорость катера из пункта А в пункт В составляет 8+2=10 (км/ч), а из пункта В в пункт А - 8-2=6(км/ч), тогда время, затраченное на преодоление пути из пункта А в пункт В - S/10, а обратно - S/6. Составим уравнение
S/10+S/6=8
Приведем к общему знаменателю
3S/30+5S/30=8
8S/30=8
Сократим обе части уравнения на 8
S/30=1
S=30 (км) - расстояние между пунктами А и В
2) Пусть S - расстояние, которое велосипедист проехал в первый день, тогда S-30 - расстояние, которое велосипедист проехал во второй день. В первый день он затратил времени - S/20, а во второй день - (S-30)/15. Составим уравнение
S/20+(S-30)/15=5
Приведем к общему знаменателю
3S/60+(4S-120)/60=5
(7S-120)/60=5
7S-120=5*60
7S=300+120
7S=420
S=60 (км) - расстояние, которое велосипедист проехал в первый день. Тогда во второй день велосипедист проехал 60-30=30 (км), а за два дня вместе 60+30=90 (км)