Нечётных цифр всего 5: 1 , 3 , 5 , 7 , 9 .
1) Надо составить четырёхзначные числа без повторения цифр.
На 1 месте (разряд тысяч) можно поставить любую из заданных пяти цифр. То есть это 5 возможностей.
На 2 месте (разряд сотен) можно поставить любую из оставшихся четырёх цифр. То есть это 4 возможности.
На 3 месте (разряд десятков) можно поставить любую из оставшихся трёх цифр. То есть это 3 возможности.
На 4 месте (разряд единиц) можно поставить любую из оставшихся двух цифр. То есть это 4 возможности.
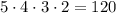
2) Надо составить четырёхзначные числа с возможностью повторения цифр.
На 1 месте (разряд десятков тысяч) можно поставить любую из заданных пяти цифр. То есть это 5 возможностей.
На 2 месте (разряд тысяч) можно поставить любую из заданных пяти цифр. То есть это 5 возможностей.
На 3 месте (разряд сотен) можно поставить любую из заданных пяти цифр. То есть это 5 возможностей.
На 4 месте (разряд единиц) можно поставить любую из заданных пяти цифр. То есть это 5 возможностей.
По правилу произведения таких трёхзначных чисел может быть
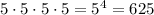
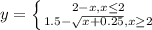
Объяснение:
Рассмотрим случай x ≤ 0
Тогда функция принимает значение

Попробуем выразить явно функцию. Для этого выделим полный квадрат в правой части:
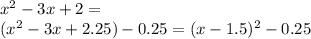
Теперь,

Для x ≤ 0 соответствует корень, взятый с отрицательным знаком. Поэтому обратная функция (просто в полученной функции меняем местами x и y), получим:
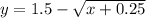 .
.
Т.к. y ≤ 0, найдем соответствующее значение x:
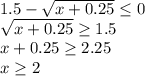
Один кусочек нашли, займемся другим
При x ≥ 0 у нас функция принимает значение:
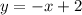
Выразим x через y, и после этого поменяем их местами

Т.е.
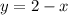
Поскольку y ≥ 0, найдем x, соответствующий этой обратной функции
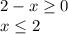
Соединяя все воедино, получим следующую кусочно-заданную функцию:
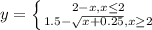
Объяснение: