Общий вид функции
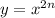
Верное свойство данной функции 3):
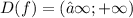
Объяснение:
Я так понимаю, имелось в виду следующее:
Дана функция
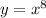
Общий вид данной функции:
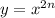
Потому что показатель степени у данной функции равен 8, т е. четный:
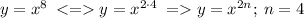
Выбери верное свойство данной функции:
1.D(f)=(−∞;0] - Неверно.
Данная функция определена как для положительных, так и для отрицательных значений аргумента
![1. \quad \: \cancel{D(f)=(−∞;0] } \\](/tpl/images/1610/0071/c3970.png)
2. Ф-ия нечётная - НЕверно
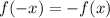
Проверим функцию на нечетность. Нечетной называется функция, если f(-x) = -f(x)
В нашем случае

3. D(f)=(−∞;+∞) - ВЕРНО!
ДАННАЯ ФУНКЦИЯ ОПРЕДЕЛЕНА ДЛЯ ЛЮБЫХ ДЕЙСТВИТЕЛЬНЫХ ЗНАЧЕНИЙ Х:
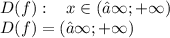
для начала находим корни данного в условии уравнения x^2-3x+1=0
D=9-4=13
x1=[3+кореньиз(13)]/2
x2=[3-кореньиз(13)]/2
Составьте уравнение корни которого на 1 больше корней уравнени:
Наши новые корни X=x1+1 и X=x2+1 получаем X=[5+кореньиз(13)]/2
X=[5-кореньиз(13)]/2
Воспользуемся теоремой Виета ,которая говорит нам: x^2+px+q=0
x1+x2=-p
x1*x2=q
Подставим в эту теорему наши новые корни (которые на 1 больше старых ):
[5+кореньиз(13)]/2+[5-кореньиз(13)]/2=-p
[5+кореньиз(13)]/2*[5-кореньиз(13)]/2=q
Таким образом наше квадратное уравнение (которое просят составить в условии) примет вид : x^2-5x+[(25-13)]/2=0-->> конечный вид x^2-5x+6=0