Из этого следует, что уравнение всегда имеет хотя бы одно решение - . Задача сводится к тому, чтобы посмотреть, при каких будут корни у уравнения и сколько их будет. Для этого достаточно рассмотреть 2 ситуации.
1) проверим, при каком значении корнем уравнения будет . Подставляем ноль в уравнение: . При имеем:
Делаем вывод, что при уравнение имеет два корня: .
2) при уравнение не может иметь корень . Уравнение - квадратное. Сразу ищем дискриминант:
Здесь рассматриваем 3 случая:
2.1. Если , то уравнение решений не имеет - следовательно, вторая скобка не будет давать новых решений и у исходного уравнения оно будет единственным.
2.2. Если , то подставляя вместо параметра -9 в итоге получаем: . Итого "вылез" еще один корень - значит, у исходного уравнения их будет два.
2.3. Если , то уравнение имеет два решения - следовательно, исходное будет иметь уже 3 решения. Заметим, что в это неравенство входит , а мы его проверяли отдельно - при корней будет 2, а не 3, поэтому из неравенства его нужно исключить.
ОТВЕТ: При уравнение имеет единственный корень; при и уравнение имеет два различных корня; при уравнение имеет три различных корня.
Решение: Высота, опущенная на гипотенузу, делит прямоугольник на два прямоугольных треугольника, где два отрезка гипотенузы прямоугольного треугольника являются проекциями катетов основного прямоугольного треугольника и кроме того они являются катетами двух образовавшихся прямоугольников. Рассмотрим один из прямоугольных треугольников, где высота, опущенная на гипотенузу является катетом (72дм), катет прямоугольника (120дм) является гипотенузой получившегося прямоугольника. По теореме Пифагора найдём другой катет (c) одного из прямоугольников: c²=120²-72² c²=14400-5184 c²=9216 c=√9216=96 (дм) - это одна из проекций катета (первого образовавшегося прямоугольного треугольника) Найдём проекцию второго катета основного прямоугольника: для этого воспользуемся свойством высоты, проведённой к гипотенузе, "высота, проведённая к гипотенузе, есть средне-геометрическое между проекциями катетов гипотенузы." Обозначим проекцию второго катета за (d) Отсюда: 72=√(96*d) 72²=96d 5184=96d d=5184 : 96 d=54 (дм-проекция второго катета) Найдём гипотенузу основного прямоугольника. Она равна сумме двух проекций катетов прямоугольного треугольника: 96+54=150 (дм) Найдём второй катет основного прямоугольника по теореме Пифагора. Известен катет, равный 120дм; гипотенуза 150дм Второй катет (b) основного прямоугольника равен: b²=150²-120² b²=22500--14400 b²=8100 b=√8100=90 (дм) - длина второго катета
ответ: Второй катет равен 90дм; проекция второго катета 54дм
Перенесем все влево и вынесем за скобки :
:
Из этого следует, что уравнение всегда имеет хотя бы одно решение - . Задача сводится к тому, чтобы посмотреть, при каких
. Задача сводится к тому, чтобы посмотреть, при каких  будут корни у уравнения
будут корни у уравнения  и сколько их будет. Для этого достаточно рассмотреть 2 ситуации.
и сколько их будет. Для этого достаточно рассмотреть 2 ситуации.
1) проверим, при каком значении корнем уравнения
корнем уравнения  будет
будет  . Подставляем ноль в уравнение:
. Подставляем ноль в уравнение: 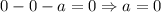 . При
. При  имеем:
имеем:
Делаем вывод, что при уравнение имеет два корня:
уравнение имеет два корня: 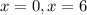 .
.
2) при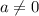 уравнение
уравнение  не может иметь корень
не может иметь корень  . Уравнение - квадратное. Сразу ищем дискриминант:
. Уравнение - квадратное. Сразу ищем дискриминант: 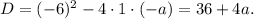
Здесь рассматриваем 3 случая:
2.1. Если , то уравнение
, то уравнение  решений не имеет - следовательно, вторая скобка не будет давать новых решений и у исходного уравнения оно будет единственным.
решений не имеет - следовательно, вторая скобка не будет давать новых решений и у исходного уравнения оно будет единственным.
2.2. Если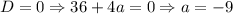 , то подставляя вместо параметра -9 в итоге получаем:
, то подставляя вместо параметра -9 в итоге получаем: 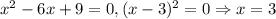 . Итого "вылез" еще один корень - значит, у исходного уравнения их будет два.
. Итого "вылез" еще один корень - значит, у исходного уравнения их будет два.
2.3. Если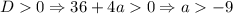 , то уравнение
, то уравнение  имеет два решения - следовательно, исходное будет иметь уже 3 решения. Заметим, что в это неравенство входит
имеет два решения - следовательно, исходное будет иметь уже 3 решения. Заметим, что в это неравенство входит  , а мы его проверяли отдельно - при
, а мы его проверяли отдельно - при  корней будет 2, а не 3, поэтому из неравенства его нужно исключить.
корней будет 2, а не 3, поэтому из неравенства его нужно исключить.
ОТВЕТ: При уравнение имеет единственный корень; при
уравнение имеет единственный корень; при 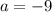 и
и  уравнение имеет два различных корня; при
уравнение имеет два различных корня; при 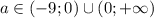 уравнение имеет три различных корня.
уравнение имеет три различных корня.