Объяснение:
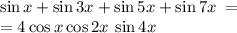
Проведем доказательство тождества следующим образом:
- проведем равносильные преобразования левой части доказываемого тождества;
- если в итоге преобразований левая часть примет ту же форму что и правая часть - тождество доказано.
Итак - левая часть:
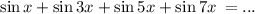
Сгруппируем следующим образом:
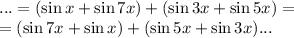
Воспользуемся формулой суммы синусов:
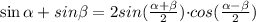
Поочередно сложим группы внутри скобок:
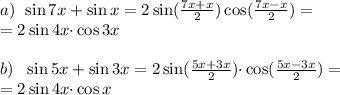
Тогда вся левая часть примет вид:
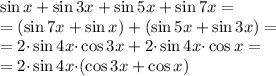
для преобразования суммы косинусов в скобках воспользуемся такой формулой:
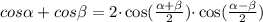
Выражение примет вид:
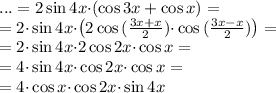
В результате преобразований левая часть приняла тот же вид что и правая.
Тождество доказано.
адо скобки писать, иначе непонятно, что на что делится.
dy/(x-1)=dx/(y-2), (y-2)dy=(x-1)dx, (y-2)^2 / 2 = (x-1)^2+C,
С находится из условия y=4 при x=0.
Объяснение: