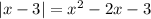, то необходимо найти область допустимых значений, то есть решить неравенство 
.
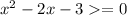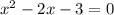
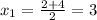
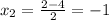
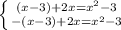
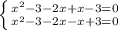
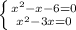
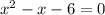
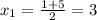=> подходит, т.к. входит в ОДЗ.
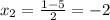=> подходит, т.к. входит в ОДЗ.
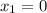=> не подходит, т.к. выходит за границы ОДЗ.
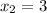=> подходит, т.к. входит в ОДЗ.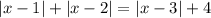
Найдём точки зануления модулей.
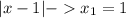
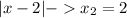
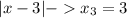
Этими тремя точками разобьём числовую прямую на 4 интервала и решим уравнение в каждом из них:
I II III IV
--------(1)--------(2)--------(3)--------
I) Раскроем модули на первом интервале (-∞; 1]: если положителен, то со знаком «+», если отрицателен, то «-»:
(1-x)+(2-x)=(3-x)+4
X=-4 => подходит, т.к. лежит в рассматриваемом интервале.
II) Раскроем модули на интервале [1; 2]:
(x-1)+(2-x)=(3-x)+4
X=6 => не подходит, так не принадлежит текущему интервалу [1; 2].
III) Раскроем модули на интервале [2; 3]:
(x-1)+(x-2)=(3-x)+4
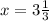=> не подходит, так не принадлежит текущему интервалу.
IV) Раскроем модули на интервале [3; ∞):
(x-1)+(x-2)=(x-3)+4
X=4 => подходит.
ответ: -4; 4.
Если число n не кратно 5, то оно дает при делении на 5 остатки либо1, либо2, либо3, либо 4, это означает, что число можно представить как
5k+1 либо 5k+2 либо 5k+3 либо 5k+4.
При n=5k+1
n-1=5k+1-1=5k - кратно 5.
Множитель (n-1) делится на 5, значит все произведение делится на 5.
При n=5k+2
n²+1=(5k+2)²+1=25k²+20k+4+1=25k²+20k+5=5(5k²+4k+1) - кратно 5.
Множитель (n²+1) делится на 5, значит все произведение делится на 5.
При n=5k+3
n²+1=(5k+3)²+1=25k²+15k+9+1=25k²+15k+10=5(5k²+3k+2) - кратно 5.
Множитель (n²+1) делится на 5, значит все произведение делится на 5.
При n=5k+4
n+1=(5k+4)+1=5k+5=5(k+1) - кратно 5.
Множитель (n+1) делится на 5, значит все произведение делится на 5.