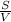Question

В группе 25 обучающихся, из которых отличников – 3, ударников – 10, остальные – слабо успевающие.
На предстоящем зачете отличники могут получить только оценки «5», ударники могут получить
с равной вероятностью оценки «4» и «5», слабо успевающие могут получить с равной
вероятностью оценки «3», «4» и «5».
Для сдачи зачета вызывается наугад один обучающийся. Какова вероятность, что он получит
оценку не ниже «4»?

Answer 1

Для начала найдём, сколько слабо успевающих учеников.

1) 25-(10+3) = 12 - слабо успевающие

Наше событие(А) - это "не ниже 4", значит, оценка 4 или 5

Обозначим вероятности (P) того, что вызванный ученик окажется или отличником(У1), или ударником(У2), или слабо успевающим(У3).

P(У1) =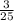 $\frac{3}{25}$

Р(У2) =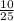 $\frac{10}{25}$

Р(У3) =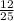 $\frac{12}{25}$

Вероятность того, что У1 ответит на оценку, не ниже 4 = 100%

Вероятность того, что У2 ответит на оценку, не ниже 4 = 100%, так как на экзамене он с равной долей вероятности получит или 4, или 5

Найдём Вероятность того, что У3 ответит на экзамене не ниже 4. С равной долей вероятности он может получить 3(О1) или 4(О2) или 5(О3). Вероятность получить одну из данных отметок равна 1/3.

P(O1)=P(O2)=P(O3)=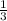 $\frac{1}{3}$

Благоприятному исходу соответствуют 2 случая: 4 или 5. Значит, вероятность получения одной из двух этих отметок равна

P(O2+O3)=P(O2)+P(O3)=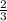 $\frac{2}{3}$

Вероятность события (А) =

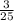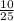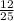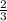P(A)=P(У1)*1+Р(У2)*1+P(У3)*P(O2+O3)= $\frac{3}{25}$ + $\frac{10}{25}$ +  $\frac{12}{25}$*$\frac{2}{3}$ =

0,12+0,4+0,32= 0,48

ответ: 0,48